class: middle, left, inverse, title-slide .title[ # Вероятности и распределения ] .subtitle[ ## Основы биостатистики, осень 2022 ] .author[ ### Марина Варфоломеева ] --- - Вероятность - Распределения вероятностей - Действия с вероятностями - Деревья вероятностей - Зависимые события - Условная вероятность - Нормальное распределение --- class: middle, center, inverse # Вероятность  ??? Начинаем разговор о неопределенности оценок. Действительно, статистика позволяет (или заставляет) говорить, что ты не уверен, и в какой именно степени не уверен в своих оценках. Вероятности чертовски важны в биологии, т.к. мы практически всегда (в 99% случаев) работаем с выборками. Свойства этих выборок во многом определяются случайностями в процессе сбора данных. --- ## Вероятность Представьте, что ваш плейлист состоит из 1000 песен и вы нажимаете кнопку `shuffle`. - Какова вероятность, что единственная самая любимая вами песня будет первой? - Какова вероятность, что первой будет не самая любимая песня? -- Представьте, что вы в лифте в 15 этажном доме, но нажали на случайную кнопку. - Какова вероятность, что вы приедете на нужный вам этаж с первой попытки? - Какова вероятность того, что вы попадете на неправильный этаж? --- ## Случайное испытание В результате случайного __испытания__ происходит или не происходит случайное __событие__. Случайному событию могут благоприятствовать один или несколько __элементарных исходов__. .pull-left-40[  Испытание: бросок шестигранного кубика Элементарные исходы: может выпасть 1, 2, 3, 4, 5, 6 Событие: на кубике выпало 4 ] -- .pull-right-60[ Испытание: нажимаем shuffle Элементарные исходы: первым может оказаться любой из треков плейлиста Событие: первый трек — любимая песня <br/> Испытание: нажимаем кнопку лифта 15-этажного дома Элементарные исходы: лифт может приехать на любой из 15 этажей Событие: попали на нужный этаж ] ??? TODO: Примеры случайных испытаний и событий: - бросаем кубик - выпало четыре - монетка - выпал орел --- ## Вероятность Вероятность события — это доля случаев, когда происходит это событие в ряду испытаний. `$$0 \le P \le 1$$` -- `\(P(A)\)` — вероятность того, что произошло некоторое событие `\(A\)`: -- - `\(P(\text{на кубике выпало 4})\)` -- - `\(P(\text{на кубике выпало четное число})\)` -- - `\(P(\text{в семье из 3 детей все девочки})\)` -- - `\(P(\text{в последовательности из 10 нуклеотидов только G})\)` -- - в случайной выборке людей оцениваем долю рыжеволосых -- - в случайной выборке новорожденных считаем долю детей с синдромом Дауна ??? TODO: Проверить фриквентистское определение вероятности --- ## Диаграмма Венна __Диаграмма Венна__ (= диаграмма Эйлера-Венна) — схематическое изображение множества (= пространства) всех элементарных исходов и его подмножеств, соответствующих определенным событиям. .pull-left[ - На кубике выпало 4  .tiny[Whitlock, Schluter, 2015, fig.5.2-1-2] ] -- .pull-right[ - На кубике выпало 3 или больше  ] -- Вероятность события легко оценить, посчитав долю элементарных исходов, благоприятствующих этому событию. --- ## Совместные и несовместные события События A и B называются __несовместными__, если `\(P(\text{A и B}) = 0\)` .pull-left[ - Выпало 4 и выпало 2 — __несовместные__ события (mutually exclusive events). ] .pull-right[ - Выпало 4 и выпало четное число — __совместные__ события. ]  --- class: middle, center, inverse # Распределения вероятностей --- ## Распределение вероятностей Все возможные исходы и их вероятности. Дискретные и непрерывные распределения вероятностей --- ## Дикретные распределения вероятностей .pull-left[ Для кубика вероятность каждого исхода — 1/6. <!-- --> ] -- .pull-right[ Для честной монетки вероятность каждого исхода — 1/2 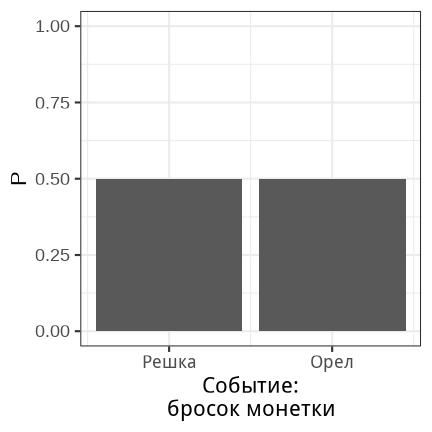<!-- --> ] -- Теоретическое распределение дискретной случайной величины `\(x\)` описывает вероятность получения определенного значения `\(x\)`. --- ## Другие примеры дискретных распределений .pull-left-40[ Распределение числа левшей в случайной выборке из 27 человек. Ожидаемая вероятность леворукости — 0.08. 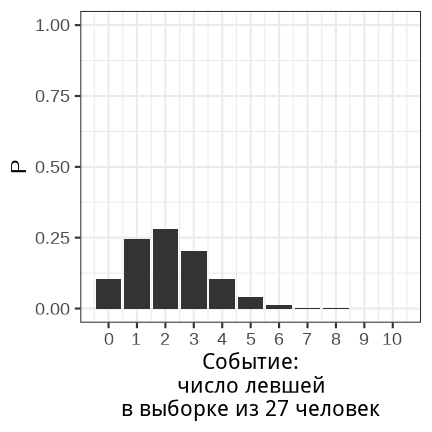<!-- --> ] -- .pull-right-60[ Распределение числа смертей в год от удара копытом лошади или мула в корпусах Прусской армии. Ожидаемая вероятность смерти от удара копытом за год в корпусе армии — 0.486. 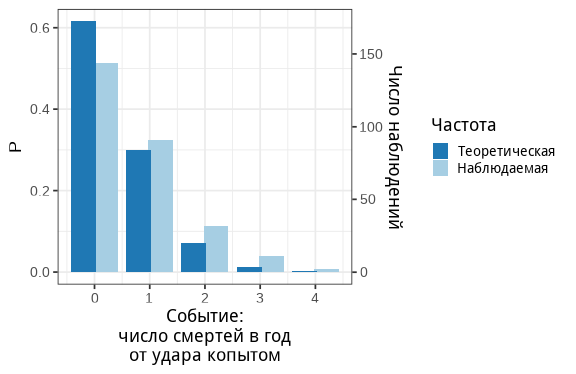<!-- --> .tiny[Данные: von Bortkiewicz, 1898; источник: пакет `pscl`] ] --- ## Непрерывные распределения вероятностей .pull-left[ 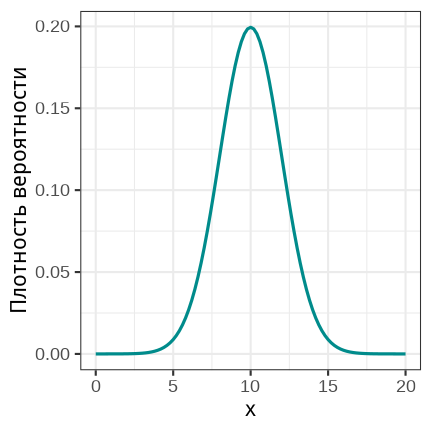<!-- --> ] .pull-right[ Описывают, какие значения может принимать непрерывная случайная величина. ] ??? Непрерывные переменные могут принимать любое значение в пределах диапазона. Т.е. между любыми двумя возможными значениями — бесконечное число других возможных значений. --- ## Относительная частота и плотность вероятности .pull-left-55[ <!-- --> ] .pull-right-45[ На "сырых" данных мы можем посчитать число наблюдений с разными значениями `\(x\)`. __Частота__ — это то, что мы бы нарисовали на гистограмме. Теоретическое распределение непрерывной случайной величины `\(x\)` описывает вероятность получить значение `\(x\)` в определенном диапазоне т.е. __плотность вероятности__. <br/> <br/> ] __Плотность вероятности__ `\(f(x)\)` — это способ задания вероятности непрерывной случайной величины `\(x\)` на любом диапазоне значений. --- ## Вероятности — площади под кривой распределения .pull-left[ <!-- --> ] .pull-right[ Площадь под всей кривой `\(= 1\)`. Вероятность встречи значений `\(x\)` из определенного промежутка можно узнать, проинтегрировав функцию распределения `\(f(x)\)`. Вероятность конкретного значения нельзя определить, т.к. это точка, а под точкой нет площади. ] --- class: middle, center, inverse # Действия с вероятностями --- ## Группы крови В среднеевропейской популяции частота встречаемости групп крови по системе AB0 представлена в таблице. .pull-left[ <br/> <table> <thead> <tr> <th style="text-align:left;"> Группа крови </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:right;"> 0.43 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:right;"> 0.42 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:right;"> 0.11 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:right;"> 0.04 </td> </tr> </tbody> </table> .tiny[[http://www.almazovcentre.ru/](http://www.almazovcentre.ru/?page_id=4595), 18.08.2022] ] .pull-right[ <!-- --> ] Нельзя иметь одновременно две группы крови по системе AB0, поэтому это несовместные события. Рассмотрим на их примере действия с вероятностями. --- ## Сложение вероятностей .content-box-grey[ Если события A и B несовместны, то вероятность того, что произойдет одно или другое — это сумма их вероятностей. `\(P(A~or~B) = P(A) + P(B)\)` ] -- <br/> Какова вероятность, что у человека кровь одной из трех групп: (A, B или AB)? .pull-left[ <br/> <table> <thead> <tr> <th style="text-align:left;"> Группа крови </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:right;"> 0.43 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:right;"> 0.42 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:right;"> 0.11 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:right;"> 0.04 </td> </tr> </tbody> </table> .tiny[[http://www.almazovcentre.ru/](http://www.almazovcentre.ru/?page_id=4595), 18.08.2022] ] -- .pull-right[ <!-- --> ] `\(P(A~or~B~or~AB) = P(A) + P(B) + P(AB) = 0.57\)` --- ## Пространство всех событий .content-box-grey[ Сумма вероятностей всех возможных несовместных событий равна 1 ] .pull-left[ <br/> <table> <thead> <tr> <th style="text-align:left;"> Группа крови </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:right;"> 0.43 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:right;"> 0.42 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:right;"> 0.11 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:right;"> 0.04 </td> </tr> </tbody> </table> .tiny[[http://www.almazovcentre.ru/](http://www.almazovcentre.ru/?page_id=4595), 18.08.2022] ] .pull-right[ <!-- --> ] `\(P(0) + P(A) + P(B) + P(AB) = 1\)` --- ## Отрицание .content-box-grey[ Вероятность того, что событие не произойдет равна 1 минус вероятность того, что оно произойдет. `\(P(not A) = 1 - P(A)\)` ] .pull-left[ <br/> <table> <thead> <tr> <th style="text-align:left;"> Группа крови </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:right;"> 0.43 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:right;"> 0.42 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:right;"> 0.11 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:right;"> 0.04 </td> </tr> </tbody> </table> .tiny[[http://www.almazovcentre.ru/](http://www.almazovcentre.ru/?page_id=4595), 18.08.2022] ] .pull-right[ <!-- --> ] `\(P(not A) = 1 - P(A) = 0.58\)` --- ## Независимые события События __независимы__, если то, что произошло одно из них, никак не влияет на то, что произойдет второе. <br/> Помимо групп крови по системе AB0 есть еще резус фактор Rh + или -. Эти признаки взаимно независимы. .pull-left[ В европейской популяции частота Rh+ 0.85. <table> <thead> <tr> <th style="text-align:left;"> Группа крови </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:right;"> 0.43 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:right;"> 0.42 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:right;"> 0.11 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:right;"> 0.04 </td> </tr> </tbody> </table> ] .pull-right[ ] --- ## Произведение независимых событий .content-box-grey[ Если события A и B независимы, то вероятность того, что произошли оба события одновременно равна произведению их вероятностей. (Это справедливо для любого числа независимых событий). `\(P(A~and~B) = P(A) \times P(B)\)` ] <br/> .pull-left[ В европейской популяции частота Rh+ 0.85. <table> <thead> <tr> <th style="text-align:left;"> Группа крови </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:right;"> 0.43 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:right;"> 0.42 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:right;"> 0.11 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:right;"> 0.04 </td> </tr> </tbody> </table> Каковы вероятности групп крови AB0 с учетом Rh (если предположить, что они независимы)? ] -- .pull-right[ <table> <thead> <tr> <th style="text-align:left;"> AB0 </th> <th style="text-align:left;"> Rh </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.366 </td> </tr> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.064 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.357 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.063 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.094 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.016 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.034 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.006 </td> </tr> </tbody> </table> ] --- ## Независимые события и их произведение В европейской популяции частота Rh+ 0.85. Каковы вероятности групп крови AB0 с учетом Rh (если предположить, что они независимы)? .pull-left[ <table> <thead> <tr> <th style="text-align:left;"> AB0 </th> <th style="text-align:left;"> Rh </th> <th style="text-align:right;"> Вероятность </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.366 </td> </tr> <tr> <td style="text-align:left;"> 0 </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.064 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.357 </td> </tr> <tr> <td style="text-align:left;"> A </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.063 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.094 </td> </tr> <tr> <td style="text-align:left;"> B </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.016 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:left;"> + </td> <td style="text-align:right;"> 0.034 </td> </tr> <tr> <td style="text-align:left;"> AB </td> <td style="text-align:left;"> – </td> <td style="text-align:right;"> 0.006 </td> </tr> </tbody> </table> ] .pull-right[ Поскольку Rh и AB0 независимы, то соотношение Rh+ и Rh- будет одинаково в каждой группе AB0. <!-- --> ] ??? Множество независимых событий: Мендель и бобы, желтые (рецессивный признак) и зеленые (доминантный признак). Можно идентифицировать гетерозигот по потомству. 3/4 потомков должны быть зеленые. Какова вероятность того, что 10 потомков гетерозиготы будут зелеными? (3/4)^10 = 0.056. Пример из Whitlock, Schluter, 2015 --- class: middle, center, inverse # Деревья вероятностей --- ## Деревья вероятностей (probability trees) Дерево вероятностей — это способ изобразить вероятности сочетаний нескольких случайных событий. <br/> В европейской популяции частота Rh+ 0.85. Какова вероятность, - что у случайно выбранного человека будет Rh-? - что у двух случайных людей будет Rh-? - что у двух случайных людей будет одинаковый резус-фактор? --- ## Нарисуем дерево вероятностей  Если речь идет об одном случайно выбранном человеке — все просто. --- ## Нарисуем дерево вероятностей  Добавляем второго случайно выбранного человека. Резус фактор второго случайно выбранного человека не зависит от первого. --- ## Нарисуем дерево вероятностей  Поскольку резус фактор второго случайно выбранного человека не зависит от первого, вероятность сочетаний этих двух независимых событий можно посчитать, перемножив вероятности. --- ## Теперь можно ответить на вопросы  .pull-left-60[ Какова вероятность, что - у случайно выбранного человека Rh-? - у двух случайных людей Rh-? - у двух случайных людей одинаковый резус-фактор? ] -- .pull-right-40[ <br/> - 0.15 - 0.0225 - 0.7225 + 0.0225 = 0.745 ] --- class: middle, center, inverse # Зависимые события --- ## Зависимые события (dependent events) События __зависимы__, если от появления одного из них зависит вероятность появления другого. По результатам мета-анализа исследований влияния курения на возникновение рака легких видно, что для курящих вероятность появления рака легких выше, чем для некурящих. Это зависимые события. .pull-left[ <br/> <table> <thead> <tr> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> <th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="2"><div style="border-bottom: 1px solid #ddd; padding-bottom: 5px; ">Smoking</div></th> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> </tr> <tr> <th style="text-align:left;"> Lung_cancer </th> <th style="text-align:right;"> Yes </th> <th style="text-align:right;"> No </th> <th style="text-align:right;"> Total </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;font-weight: bold;"> Yes </td> <td style="text-align:right;"> 17393 </td> <td style="text-align:right;"> 433 </td> <td style="text-align:right;font-weight: bold;"> 17826 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;"> No </td> <td style="text-align:right;"> 2043 </td> <td style="text-align:right;"> 8527 </td> <td style="text-align:right;font-weight: bold;"> 10570 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;font-weight: bold;"> Total </td> <td style="text-align:right;font-weight: bold;"> 19436 </td> <td style="text-align:right;font-weight: bold;"> 8960 </td> <td style="text-align:right;font-weight: bold;font-weight: bold;"> 28396 </td> </tr> </tbody> </table> .tiny[Данные Barukčić, 2019, table 7; DOI: [10.22270/jddt.v9i1-s.2273](https://doi.org/10.22270/jddt.v9i1-s.2273)] ] .pull-right[ <!-- --> ] ??? Barukčić, I. (2019). Smoking of tobacco is the cause of human lung cancer. Journal of Drug Delivery and Therapeutics, 9(1-s), 148-160. DOI: [10.22270/jddt.v9i1-s.2273](https://doi.org/10.22270/jddt.v9i1-s.2273) --- ## Задание .pull-left-40[ Нарисуйте дерево вероятностей <table> <thead> <tr> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> <th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="2"><div style="border-bottom: 1px solid #ddd; padding-bottom: 5px; ">Smoking</div></th> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> </tr> <tr> <th style="text-align:left;"> Lung_cancer </th> <th style="text-align:right;"> Yes </th> <th style="text-align:right;"> No </th> <th style="text-align:right;"> Total </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;font-weight: bold;"> Yes </td> <td style="text-align:right;"> 17393 </td> <td style="text-align:right;"> 433 </td> <td style="text-align:right;font-weight: bold;"> 17826 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;"> No </td> <td style="text-align:right;"> 2043 </td> <td style="text-align:right;"> 8527 </td> <td style="text-align:right;font-weight: bold;"> 10570 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;font-weight: bold;"> Total </td> <td style="text-align:right;font-weight: bold;"> 19436 </td> <td style="text-align:right;font-weight: bold;"> 8960 </td> <td style="text-align:right;font-weight: bold;font-weight: bold;"> 28396 </td> </tr> </tbody> </table> ] -- .pull-right-60[  ] .pull-left-40[ <br/><br/><br/> Вероятность курения/некурения среди всех: `\(P_{курит = да} =\)` `\(P_{курит = нет} =\)` ] .pull-right-60[ Вероятность рака среди курящих: `\(P_{рак = да | курит = да} =\)` `\(P_{рак = нет | курит = да} =\)` <br/> Вероятность рака среди некурящих: `\(P_{рак = да | курит = нет} =\)` `\(P_{рак = нет | курит = нет} =\)` ] --- ## Решение .pull-left-40[ <br/> <table> <thead> <tr> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> <th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="2"><div style="border-bottom: 1px solid #ddd; padding-bottom: 5px; ">Smoking</div></th> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> </tr> <tr> <th style="text-align:left;"> Lung_cancer </th> <th style="text-align:right;"> Yes </th> <th style="text-align:right;"> No </th> <th style="text-align:right;"> Total </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;font-weight: bold;"> Yes </td> <td style="text-align:right;"> 17393 </td> <td style="text-align:right;"> 433 </td> <td style="text-align:right;font-weight: bold;"> 17826 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;"> No </td> <td style="text-align:right;"> 2043 </td> <td style="text-align:right;"> 8527 </td> <td style="text-align:right;font-weight: bold;"> 10570 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;font-weight: bold;"> Total </td> <td style="text-align:right;font-weight: bold;"> 19436 </td> <td style="text-align:right;font-weight: bold;"> 8960 </td> <td style="text-align:right;font-weight: bold;font-weight: bold;"> 28396 </td> </tr> </tbody> </table> <br/><br/><br/> Вероятность курения/некурения среди всех: `\(P_{курит = да} = 19436/28396 = 0.684\)` `\(P_{курит = нет} = 8960/28396 = 0.316\)` ] .pull-right-60[  Вероятность рака среди курящих: `\(P_{рак = да | курит = да} = 17393/ 19436 = 0.895\)` `\(P_{рак = нет | курит = да} = 2043/ 19436 = 0.105\)` <br/> Вероятность рака среди некурящих: `\(P_{рак = да | курит = нет} = 433/ 8960 = 0.048\)` `\(P_{рак = нет | курит = нет} = 8527/ 8960 = 0.952\)` ] --- ## Дерево вероятностей для этих данных .pull-left-60[  ] .pull-right-40[ <!-- --> ] -- <br/> __Осторожно!__ Поскольку события "курение" и "рак легких" — зависимые, правило умножения не выполняется: `\(P(курение~и~рак) \ne P(курение) \times P(рак)\)` -- <br/> На самом деле `\(P(курение~и~рак) = 0.612\)`. А если ошибочно считать по формуле для независимых событий, то `\(P(курение) \times P(рак) = 0.684 \times (0.895 + 0.0483) = 0.645\)`. --- class: middle, center, inverse # Условная вероятность --- ## Условная вероятность (conditional probability) __Условная вероятность__ — вероятность события, при каком-то условии (например, при условии, что произошло какое-то другое событие или события). .pull-left-60[  ] .pull-right-40[ <br/> <!-- --> ] -- `\(P(рак = да|курит = да) = 0.895\)` — вероятность рака легких при условии, что человек курит `\(P(рак = да |курит = нет) = 0.0483\)` — вероятность рака легких при условии, что человек НЕ курит --- ## Формула полной вероятности <br/> (law of the total probability) .content-box-grey[ Вероятность события `\(A\)` можно вычислить исходя из его вероятностей при условии каждого из несовместных событий `\(B_i\)`. `$$P(A) = \sum_{i = 1}^{n} P(A|B_i) P(B_i)$$` ] .pull-left-55[  ] .pull-right-45[ <!-- --> ] -- И действительно, вероятность того, что у случайно выбранного человека рак, будет складываться из площадей красных прямоугольников. ??? Т.е. как будто у нас получается взвешенное среднее вероятности A при всех несовместных событиях. Иначе можно сказать, что априорная вероятность события равна среднему его апостериорной вероятности. --- ## Обобщенное правило умножения вероятностей <br/>(generel multiplication rule) .content-box-grey[ Вероятность того, что произошли оба события, даже если они зависимы `$$P(A~and~B) = P(A) \cdot P(B|A) = \\ = P(B) \cdot P(A|B)$$` ] .pull-left-55[  ] .pull-right-45[ <!-- --> ] --- ## Задание В 80-е годы в канаде 52% взрослых мужчин курили. По оценкам исследователей вероятность развития рака лежких в течение жизни у мужчин курильщиков была 17.2 %, а у некурящих 1.2 % (Villneuve and Mao, 1994). <br/> - Какова условная вероятность нажить себе рак для канадца, если он курил в 80е годы? <br/><br/> - Какова вероятность того, что канадец курил в 80-е годы и у него развился рак? <br/><br/> - Какова вероятность того, что канадец не курил в 80-е годы и не получил рак? <br/><br/> -- Используйте обобщенное правило умножения вероятностей `$$P(A~and~B) = P(A) \cdot P(B|A) = \\ = P(B) \cdot P(A|B)$$` -- Ради интереса и самопроверки, нарисуйте дерево вероятностей и сравните результаты. --- ## Решение В 80-е годы в канаде 52% взрослых мужчин курили. По оценкам исследователей вероятность развития рака легких в течение жизни у мужчин курильщиков была 17.2 %, а у некурящих 1.2 % (Villneuve and Mao, 1994). <br/> - Какова условная вероятность нажить себе рак для канадца, если он курил в 80е годы? `\(P_{рак|курильщик} = 0.172\)` - Какова вероятность того, что канадец курил в 80-е годы и у него развился рак? `\(P_{курильщик~и~рак} = P_{курильщик} \times P_{рак|курильщик} = 0.52 \times 0.172 = 0.089\)` - Какова вероятность того, что канадец не курил в 80-е годы и не получил рак? `\(P_{курильщик~и~нет~рака} = P_{некурящий} \times P_{нет~ рака|некурящий} = 0.48 \times 0.987 = 0.474\)` Обобщенное правило умножения вероятностей `$$P(A~and~B) = P(A) \cdot P(B|A) = \\ = P(B) \cdot P(A|B)$$` --- class: middle, center, inverse # Нормальное распределение  --- ## Частотные распределения мерных признаков <!-- --> Частотные распределения многих мерных признаков имеют колоколообразную форму. --- ## Нормальное распределение <!-- --> Теоретическое распределение, которое описывает многие из таких колоколообразных кривых, называется __нормальное распределение__. --- ## Нормальное распределение .pull-left[ <!-- --> ] .pull-right[ Нормальное распределение - Симметричное - Унимодальное - Непрерывное - Наибольшая плотность вероятности — там, где среднее значение - `\(-\infty \le x \le \infty\)` ] --- ## Формула нормального распределения .pull-left[ <!-- --> ] .pull-right[ `$$f(x) = \cfrac {1}{\sigma \sqrt{2 \pi}} \; e^{- \: \cfrac{(x-\mu)^2}{2\sigma^2}}$$` Параметры:<br/> - `\(\mu\)` --- среднее значение <br/> <br/> - `\(\sigma\)` --- стандартное отклонение ] Случайная величина `\(x\)` подчиняется нормальному распределению со средним `\(\mu\)` и стандартным отклонением `\(\sigma\)`. Это кратко записывается как `\(x \sim N(\mu, \sigma)\)`. --- ## Параметры нормального распределения .pull-left[ <!-- --> ] .pull-right[ `$$f(x) = \cfrac {1}{\sigma \sqrt{2 \pi}} \; e^{- \: \cfrac{(x-\mu)^2}{2\sigma^2}}$$` Параметры:<br/> - `\(\mu\)` --- среднее значение — задает положение вершины по оси Х <br/> - `\(\sigma\)` --- стандартное отклонение — задает размах кривой распределения ] -- .pull-left[ На рисунке распределения: - `\(x_1 \sim N(\mu_1, \sigma_1)\)` - `\(x_2 \sim N(\mu_2, \sigma_2)\)` ] .pull-right[ Параметры этих распределений: - `\(\mu_1 < \mu_2\)` - `\(\sigma_1 > \sigma_2\)` ] --- ## Кривые распределений можно использовать <br/>для оценки вероятностей <!-- --> --- ## Площадь под всей кривой распределения равна 1 <br/><br/> <!-- --> --- ## Вероятность конкретного значения нельзя определить <br/><br/> <!-- --> --- ## Можно определить вероятность того, <br/>что значение будет меньше заданного <!-- --> --- ## Остальные площади можно найти <br/>при помощи арифметических действий <!-- --> --- ## Задание .pull-left-60[ Распределение диаметра колоний бактерий  ] .pull-right-40[ Какова вероятность, что диаметр случайно выбранной колонии будет лежать в заданных пределах? - между 4 и 6 мм - между 8 и 12 мм <br/> <br/> - больше 10 мм <br/> <br/> - между 8 и 10 мм <br/> <br/> - меньше 6 мм <br/> <br/> - меньше 4 или больше 12 мм ] .pull-down[.tiny[Whitlock and Shluter 2015, p.146]] --- ## Решение .pull-left-60[ Распределение диаметра колоний бактерий  ] .pull-right-40[ Какова вероятность, что диаметр случайно выбранной колонии будет лежать в заданных пределах? - между 4 и 6 мм `\(P = 0.14\)` - между 8 и 12 мм `\(P = 0.48\)` <br/> <br/> - больше 10 мм `\(P = 0.14 + 0.02 = 0.16\)` - между 8 и 10 мм `\(P = 0.48 - 0.14 = 0.34\)` - меньше 6 мм `\(P = 0.14 + 0.02 = 0.16\)` - меньше 4 или больше 12 мм `\(P = 0.02 + 0.02\)` ] .pull-down[.tiny[Whitlock and Shluter 2015, p.146]] --- ## Площади под кривой нормального распределения .pull-left[ <!-- --> ] .pull-right[ Правило 68--95--99.7 % Если по оси `\(x\)` отложить стандартные отклонения от среднего значения, то окажется, что приблизительно - `\(\sim\)` 68% значений в пределах `\(1\;\sigma\)` - `\(\sim\)` 95% --- в пределах `\(2\;\sigma\)` - `\(\sim\)` 99.7% --- в пределах `\(3\;\sigma\)` ] --- class: middle, center, inverse # Summary --- ## Summary: основные действия с вероятностями - Вероятность события это доля случаев, когда это событие происходит в ряду повторных испытаний. - Распредедение вероятностей описывает вероятности различных исходов случайного испытания. - События называются несовместными, если не могут произойти одновременно. - Суммарная вероятность всех несовместных событий равна 1. - Вероятность того, что произойдет хотя бы одно из двух несовместных событий, равна сумме их вероятностей. - Вероятность того, что произойдет одно из двух необязательно несовместных событий равна сумме их вероятностей за вычетом вероятности того, что они произошли оба. --- ## Summary: зависимые и независимые события - Деревья вероятностей помогают записать и вычислить вероятности цепочек событий. - Условная вероятность события - это вероятность события, при условии, что уже произошло какое-то другое событие. - Вероятность того, что произошли одновременно два независимых события, равна произведению их вероятностей. - Вероятность того, что произошли два зависимых события, равна произведению полной вероятности одного из них на вероятность другого при условии, что первое произошло. - Формула полной вероятности гласит, что вероятность события можно вычислить как сумму его вероятностей при условии каждого из несовместных событий. --- ## Summary: нормальное распределение - Нормальное распределение имеют многие мерные величины. - Параметры нормального распределения задают положение его центра (среднее) и разброс (стандартное отклонение). - Площади под кривой нормального распределения можно использовать для вычисления вероятности того, что значение нормально распределенной величины попадает в определенный диапазон, если известны параметры распределения этой величины в генеральной совокупности. --- ## Что почитать - Bluman, A. G. (2005). Probability Demystified (Vol. 1). McGraw-Hill Professional. - Whitlock, M., & Schluter, D. (2015). The analysis of biological data (Second edition)**. Roberts and Company Publishers.