Корреляция и регрессия

.title[
# Корреляция и регрессия
]
.subtitle[
## Основы биостатистики, осень 2022
]
.author[
### Марина Варфоломеева
]

---

- Корреляция
- Простая линейная регрессия
- Условия применимости линейной регрессии

---

# Корреляция

---

## Пример: львиные носы

Определение возраста львов на расстоянии важно, чтобы решить, на кого можно охотиться.

Есть ли связь между степенью пигментации львиного носа и возрастом льва? (данные Whitman et al., 2004)

---

## Пример: инбридинг у волков

В 70-80 волки в Норвегии и Швеции прошли через бутылочное горлышко. Популяция восстановилась всего от пары особей, поэтому можно ожидаемо наблюдать последствия инбридинга.

Связан ли коэффициент инбридинга и число волчат в выводке, переживших свою первую зиму? (данные Liberg et al, 2005)

---

## Корреляция

Когда переменные взаимосвязаны друг с другом, говорят, что между ними есть корреляция.

]
.pull-right[

]

---

## Корреляция

Когда переменные взаимосвязаны друг с другом, говорят, что между ними есть корреляция.

Положительная корреляция — чем больше одна величина, тем больше другая.

]

.pull-right[
<img src="21-correlation-and-regression_files/figure-html/gg-wolves-1.png" width="432" />

Отрицательная корреляция — чем больше одна величина, тем меньше другая.
]

---

## Коэффициент корреляции Пирсона

— оценивает силу и направление связи между численными величинами.

`$$r=\cfrac{\sum_i\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_i\left(x_i-\bar{x}\right)^2} \sqrt{\sum_i\left(y_i-\bar{y}\right)^2}}$$`

В числителе — сумма произведений __отклонений__ переменных от их средних.

`$-1 < r < 1$`  
- `$|r| = 1$` --- сильная связь
--
: `$r > 0$` — положительная, `$r < 0$` — отрицательная

--
- `$r = 0$` --- нет связи

---

## Корреляция на графике

---

## Стандартная ошибка коэффициента корреляции

`$r$` — корреляция, расчитаная по данным, это оценка истинного значения корреляции `$\rho$` в генеральной совокупности.

Стандартная ошибка этой оценки:

`$$\mathrm{SE}_r=\sqrt{\frac{1-r^2}{n-2}}$$`

Ее не получится использовать для доверительного интервала, т.к. ее выборочное распределение не нормально.

Но ее можно использовать для тестов.

---

## Приблизительный доверительный интервал

Z-преобразование Фишера:

`$z = 0.5 \ln \left(\cfrac{1+ r}{1-r}\right)$`

Стандартная ошибка выборочного распределения `$z$`

`$SE_z=\sqrt{\frac{1}{n-3}}$`

Доверительный интервал для Z-преобразованного значения корреляции

`$z - 1.96 \cdot SE_z < z < z + 1.96 \cdot SE_z$`

Границы нужно трансформировать обратно из `$z$` шкалы в `$r$`, чтобы получить доверительный интервал для `$r$`

`$r = \cfrac{\mathrm{e}^{2 z}-1}{\mathrm{e}^{2 z}+1}$`

---

## Тестирование значимости коэффициента корреляции

`$H_0: \rho = 0$` — нет связи между переменными (в генеральной совокупности корреляция `$\rho$` между ними равна нулю)

`$H_A: \rho \ne 0$` — между переменными есть связь

`$$t=\cfrac{r - 0}{\mathrm{SE}_r}$$`

`$df = n - 2$`

---

## Условия применимости коэффициента корреляции Пирсона

(1) Двумерное нормальное распределение переменных (требуется для работы тестов значимости)

![](img/WS2015p513f16.3-1.png)

---

## Условия применимости коэффициента корреляции Пирсона

(2) Не должно быть гетерогенности дисперсий

(3) В данных не должно быть выбросов (= outliers)

(4) Связь должна быть линейной. Если связь нелинейна, то коэффициент корреляции Пирсона оценит только ее линейную составляющую.

![](img/WS2015p514f16.3-2.png)

---

## Если нарушены условия применимости

Что можно сделать:

- выбросы можно удалить, если есть аргументы в пользу этого
- трансформация данных может помочь:
  - для линеаризации зависимости
  - для нормализации формы распределения

В других случаях ранговые коэффициенты корреляции:

- кор. Кендалла
- кор. Спирмена,  
и т.д.

---

# Линейная регрессия

---

## Линейная регрессия

- позволяет описать зависимость между количественными величинами
- позволяет предсказать значение одной величины, зная значения других

.center[
<img src="21-correlation-and-regression_files/figure-html/gg-lions-lm-1.png" width="432" />
]

---

## Уравнение линейной регрессии

.center[
<img src="21-correlation-and-regression_files/figure-html/gg-lions-lm-1.png" width="432" />
]

В выборке

`$$y _i = b _0 + b _1 x _i + e_i$$`

]

В генеральной совокупности

`$$y _i = \beta _0 + \beta _1 x _{1i} + \varepsilon_i$$`

]

---

## Линейная регрессия бывает простая и множественная

- простая

`$$y _i = \beta _0 + \beta _1 x _i + \varepsilon _i$$`

- множественная

`$$y _i = \beta _0 + \beta _1 x _{1 i} + \beta _2 x _{2 i} + ... + \varepsilon _i$$`

---

## Коэффициенты линейной регрессии

]
.pull-right[

`$$y _i = b _0 + b _1 x _i + e_i$$`

- `$y_i$` — наблюдаемое значение (= observed) зависимой переменной, отклик
- `$x_i$` — значение независимой переменной, предиктор (=predictor)
- `$\hat y_i$` — предсказанное значение (= fitted, predicted) зависимой переменной
- `$e_i$` — остатки (= residuals), отклонения наблюдаемых от предсказанных значений

]

- `$b_0$` — свободный член линейной модели, отрезок (intercept), отсекаемый регрессионной прямой на оси `$y$`
- `$b_1$` — коэффициент угла наклона (slope) регрессионной прямой

---

## Как провести линию регрессии?

]
.pull-right[

`$$\hat y _i = b _0 + b _1 x _i$$`

Нужно получить `$b_0$` и `$b_1$` — оценки истинных параметров линейной модели `$\beta _0$` и `$\beta _1$`.

]

---
layout: true
class: split-30
.row[.content[

## Линия должна проходить как можно ближе к точкам

]]

.row[.content[.split-three[
.column[.content[
<img src="21-correlation-and-regression_files/figure-html/unnamed-chunk-4-1.png" width="324" />

]]
.column[.content[
<img src="21-correlation-and-regression_files/figure-html/unnamed-chunk-5-1.png" width="324" />

]]
.column[.content[
<img src="21-correlation-and-regression_files/figure-html/unnamed-chunk-6-1.png" width="324" />

]]
]]]

---

---

---

---

---
layout: false

## Метод наименьших квадратов

`$$\hat y _i = b _0 + b _1 x _i$$`

Значения коэффициентов `$b_0$` и `$b_1$` подбирают так, чтобы минимизировать __сумму квадратов остатков__  `$\sum{e^2_i}$`, т.е. `$MS_e = \sum{(y _i - \hat y _i)^2}$`.

---

## Оценки параметров линейной регрессии

|Параметр   |  Оценка  |  Стандартная ошибка |
|----|----|----|
| `$\beta_0$`  |  `$b_0 = \bar y - b_1 \bar{x}$`   |  `$SE _{b _0} = \sqrt{MS _e [\cfrac{1}{n} + \cfrac{\bar x}{\sum {(x _i - \bar x)^2}}]}$`|
| `$\beta_1$`  |  `$b _1 = \cfrac {\sum {[(x _i - \bar {x})(y _i - \bar {y})]}}{\sum {(x _i - \bar x)^2}}$`  |  `$SE _{b _1} = \sqrt{\cfrac{MS _e}{\sum {(x _i - \bar {x})^2}}}$` |
| `$\varepsilon _i$`  |  `$e_i = y_i - \hat {y}_i$`  |  `$\approx \sqrt{MS_e}$` |

Оценки коэффициентов

- позволяют получить предсказанные значения

Стандартные ошибки коэффициентов

- используются для построения доверительных интервалов
  - нужны для статистических тестов

---

## Линейная регрессия в примере про львов

В общем виде линейная регрессия:

`$$\hat y _i = b _0 + b _1 x _i$$`

В примере про львов:

`$$\widehat{Возраст}_i = b _0 + b _1 \cdot \text{Доля черного}_i$$`

Мы подобрали коэффициенты модели методом наименьших квадратов:

<table>
 <thead>
  <tr>
   <th style="text-align:left;">   </th>
   <th style="text-align:right;"> Значение коэффициента </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> `$b_0$` </td>
   <td style="text-align:right;"> 0.879 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> `$b_1$` </td>
   <td style="text-align:right;"> 10.647 </td>
  </tr>
</tbody>
</table>

Получилось уравнение:

`$$\widehat{Возраст}_i = 0.88 + 10.65 \cdot \text{Доля черного}_i$$`

Смысл коэффициентов:

- `$b_0 = 0.88$` — Ожидаемый возраст льва с непигментированным носом 0.88 лет.
- `$b_1 = 10.65$` — Если доля черного увеличится на единицу, ожидаемый возраст льва увеличится на 10.65 лет.

---

## Доверительный интервал коэффициента регрессии

__Доверительный интервал коэффициента__ --- это зона, в которой при повторных выборках из генеральной совокупности с заданной вероятностью будет лежать среднее значение оценки коэффициента.

Если `$\alpha = 0.05$`, то получается 95% доверительный интервал.

`$$b _1 \pm t _{\alpha, df = n - 2} \cdot SE _{b _1}$$`

------

В примере про львов  стандартные ошибки для каждого из коэффициентов:

<table>
 <thead>
  <tr>
   <th style="text-align:left;">   </th>
   <th style="text-align:right;"> Значение коэффциента </th>
   <th style="text-align:right;"> SE </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> `$b_0$` </td>
   <td style="text-align:right;"> 0.879 </td>
   <td style="text-align:right;"> 0.569 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> `$b_1$` </td>
   <td style="text-align:right;"> 10.647 </td>
   <td style="text-align:right;"> 1.510 </td>
  </tr>
</tbody>
</table>

`$df = 32 - 2 = 30$`

`$t_{30} = 2.04$`

Доверительные интервалы

Для `$b_0$`:

`$0.879 \pm 2.04 \cdot 0.569$`  
`$0.879 \pm 1.16$`

]

Для `$b_1$`:

`$10.647 \pm 2.04 \cdot 1.51$`  
`$10.647 \pm 3.08$`

]

---

## Доверительная зона регрессии

__Доверительная зона регрессии__ --- это зона, в которой при повторных выборках из генеральной совокупности с заданной вероятностью лежит регрессионная прямая.

95% доверительная зона

]

99% доверительная зона

]

---

# Предсказываем с помощью регрессии

---

## Предсказания при помощи регрессии

В примере про львов получилось уравнение:

`$\widehat{Возраст}_i = 0.88 + 10.65 \cdot \text{Доля черного}_i$`

Исследователь мог заметить в бинокль нового льва с долей черного на носу 0.5.

Ожидаемый возраст: `$0.88 + 10.65 \cdot 0.5 = 6.2$`

<img src="21-correlation-and-regression_files/figure-html/lion-conf-int-1.png" width="468" />
]

.pull-right[
На линии регрессии лежат ожидаемые средние значения `$y$` при разных значениях `$x$`. В доверительный интервал для этих средних  попадет __среднее значение возраста львов в 95% повторных выборок__.

]

---

## Неопределенность оценки предсказаний

__Доверительный интервал для предсказаний__ --- это зона, в которую попадут индивидуальные наблюдения `$\hat y _i$` при данном `$x _i$` в заданной доле повторных выборок.

`$\hat y _i \pm t _{\alpha, n - 2} \cdot SE _{\hat y _i}$`,

где `$SE _{\hat y} = \sqrt{MS _{e} [1 + \frac{1}{n} + \frac{(x _{prediction} - \bar x)^2} {\sum _{i=1}^{n} {(x _{i} - \bar x)^2}}]}$`

-----

В примере про львов

<img src="21-correlation-and-regression_files/figure-html/lion-pred-int-1.png" width="468" />
]
.pull-right[

На линии регрессии лежат ожидаемые средние значения `$y$` при разных значениях `$x$`. В доверительный интервал предсказаний попадет __наблюдаемый возраст львов в 95% повторных выборок__.

]

---

## Доверительная область значений

__Доверительная область значений__ --- это зона, в которую попадают наблюдения в `$(1 - \alpha) \cdot 100\%$` повторных выборок

---

## Важно!

![:scale 90%](img/xkcd_husbands.png)

---

## Интерполяция и экстраполяция

Модель "работает" только в том диапазоне значений независимой переменной `$x$`, для которой она построена (интерполяция).

Экстраполяцию надо применять с большой осторожностью.

---

# Тестирование значимости модели и ее коэффициентов

---

## Способы проверки значимости модели и ее коэффициентов

Существует несколько способов проверки значимости модели

Значима ли модель целиком?

+ F критерий: действительно ли объясненная моделью изменчивость больше, чем случайная (=остаточная) изменчивость

Значима ли связь между предиктором и откликом?

+ t-критерий: отличается ли от нуля коэффициент при этом предикторе
+ F-критерий: значимо ли отличаются модели с даным предиктором и без него?

---

## Тестируем значимость коэффициентов t-критерием

`$$t = \frac{b _1 - 0}{SE _{b _1}}$$`

`$H _0 : b _1 = 0$`  
`$H _A : b _1 \ne 0$`

`$t$`-статистика подчиняется `$t$`-распределению с числом степеней свободы `$df = n - p$`, где `$p$` --- число параметров.

Для простой линейной регрессии `$df = n - 2$`.

---

## Тестируем значимость коэффициентов t-критерием

.small[
<table>
 <thead>
  <tr>
   <th style="text-align:left;">   </th>
   <th style="text-align:right;"> Estimate </th>
   <th style="text-align:right;"> Std. Error </th>
   <th style="text-align:right;"> t value </th>
   <th style="text-align:right;"> Pr(&gt;|t|) </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> 0.879 </td>
   <td style="text-align:right;"> 0.569 </td>
   <td style="text-align:right;"> 1.54 </td>
   <td style="text-align:right;"> 0.133 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> proportionBlack </td>
   <td style="text-align:right;"> 10.647 </td>
   <td style="text-align:right;"> 1.510 </td>
   <td style="text-align:right;"> 7.05 </td>
   <td style="text-align:right;"> 0.000 </td>
  </tr>
</tbody>
</table>
]

Результаты можно описать в тексте так:

Возраст льва статистически значимо зависит от количества черного пигмента на носу ( `$b _1 = 10.65$`, `$t_{df=30} = 7.05$`, `$p < 0.01$` )

---

# Тестирование гипотез <br/>при помощи F-критерия

---

## Общая изменчивость

Общая изменчивость `$SS_{t}$` — это сумма квадратов отклонений наблюдаемых значений `$y_i$` от общего среднего `$\bar y$`

---

## Структура общей изменчивости

`$$SS_t = \color{purple}{SS_r} + \color{green}{SS_e}$$`

---

## От изменчивостей к дисперсиям

| `$MS_t$`, полная дисперсия | `$\color{purple}{MS_r}$`, дисперсия, <br /> объясненная регрессией  | `$\color{green}{MS_e}$`, остаточная дисперсия | 
|-----|-----|-----|
| `$MS_{t} =\frac{SS_{t}}{df_{t}}$` | `$\color{purple}{MS_{r}} =\frac{\color{purple}{SS_{r}}}{df_{r}}$` | `$\color{green}{MS_{e}} =\frac{\color{green}{SS_{e}}}{df_{e}}$` |
| `$SS_{t}=\sum{(y_i - \bar{y})^2}$` | `$\color{purple}{SS_{r}}=\sum{(\hat{y}-\bar{y})^2}$` | `$\color{green}{SS_{e}}=\sum{(y_i - \hat{y})^2}$` |
| `$df_{t} = n-1$` | `$df_{r} = 1$` | `$df_{e} = n-2$`  |

---

## С помощью `$MS_r$` и `$MS_e$` можно тестировать значимость коэффициентов

Если зависимости нет, то `$\color{purple}{MS_r} \approx \color{green}{MS_e}$`

- `$H_0: \color{}{\beta_1} = 0$`
- `$H_A: \color{}{\beta_1} \ne 0$`

`$$F_{df_r, df_e}= \frac{\color{purple}{MS _{r}}}{\color{green}{MS_{e}}}$$`

---

## Тестирование значимости коэффициентов регрессии при помощи F-критерия

`$$F_{df_r, df_e}= \frac{\color{purple}{MS _{r}}}{\color{green}{MS_{e}}}$$`

Для простой линейной регрессии  
`$df_{r} = 1$` и `$df_{e} = n - 2$`

]

F-тест будет односторонним, т.к. соотношение дисперсий может быть только положительным.

]

---

## Таблица результатов дисперсионного анализа

| Источник изменчивости  | df | SS | MS | F  | 
| ----- | ----- | ----- | ----- | ----- | 
| .purple[Регрессия] | `$df _r = 1$` | `$\color{purple}{SS _r} = \sum{(\hat y _i - \bar y)^2}$` | `$\color{purple}{MS _r} = \frac{\color{purple}{SS _r}}{df _r}$` | `$F _{df _r, df _e} = \frac{\color{purple}{MS _r}}{\color{green}{MS _e}}$` | 
| .green[Остаточная]|  `$df _e = n - 2$` | `$\color{green}{SS _e} = \sum{(y _i - \hat y _i)^2}$` | `$\color{green}{MS _e} = \frac{\color{green}{SS _e}}{df _e}$` | 
| Общая | `$df _t = n - 1$` | `$SS _t = \sum {(y _i - \bar y)^2}$` |

Минимальное упоминание результатов в тексте должно содержать `$F _{df _r, df _e}$` и `$p$`.

---

## Проверяем значимость модели при помощи F-критерия

<table>
 <thead>
  <tr>
   <th style="text-align:left;">   </th>
   <th style="text-align:right;"> Sum Sq </th>
   <th style="text-align:right;"> Df </th>
   <th style="text-align:right;"> F value </th>
   <th style="text-align:right;"> Pr(&gt;F) </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> proportionBlack </td>
   <td style="text-align:right;"> 138.5 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 49.8 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Residuals </td>
   <td style="text-align:right;"> 83.5 </td>
   <td style="text-align:right;"> 30 </td>
   <td style="text-align:right;">  </td>
   <td style="text-align:right;">  </td>
  </tr>
</tbody>
</table>

Результаты дисперсионного анализа можно описать в тексте (или представить в виде таблицы):

- Возраст льва статистически значимо зависит от количества черного пигмента на носу ( `$F _{1, 30} = 49.75$`, `$p < 0.001$`).

---

# Оценка качества подгонки модели

---

## В чем различие между этими двумя моделями?

У этих моделей разный разброс остатков:

- Модель слева объясняет практически всю изменчивость
- Модель справа объясняет не очень много изменчивости

---

## Коэффициент детерминации — мера качества подгонки модели

__Коэффициент детерминации__ описывает какую долю дисперсии зависимой переменной объясняет модель

`$$R^2 = \frac{\color{purple}{SS_{r}}}{SS_{t}}$$`

- `$0 < R^2 < 1$`
- `$R^2 = r^2$` — для простой линейной регрессии коэффициент детерминации равен квадрату коэффициента Пирсоновской корреляции

---

## Если в модели много предикторов, нужно внести поправку

__Скорректированный коэффициет детерминации__ (adjusted R-squared)

Применяется если необходимо сравнить две модели с разным количеством параметров

$$ R^2_{adj} = 1- (1-R^2)\frac{n-1}{n-p}$$

`$p$` - количество параметров в модели

Вводится штраф за каждый новый параметр

---

# Условия применимости простой линейной регрессии

---

## Условия применимости простой линейной регрессии

Условия применимости линейной регрессии должны выполняться, чтобы тестировать гипотезы

1. Независимость наблюдений
1. Линейность связи
1. Нормальное распределение остатков
1. Равенство дисперсий остатков

Для множественной линейной регрессии добавляется требование независимости предикторов друг от друга (отсутствие мультиколлинеарности).

---

## 1. Независимость наблюдений

- Значения `$y _i$` должны быть независимы друг от друга
- Берегитесь псевдоповторностей и автокорреляций (например, временных)
- Контролируется на этапе планирования
- Проверяем на графике зависимости остатков от предсказанных значений

![](images/assumption-12.png)

---

## 2. Линейность связи

- Проверяем на графике зависимости остатков от предсказанных значений

![](images/assumption-12.png)

---

## 3. Нормальное распределение остатков

Нужно, т.к.

`$Y _i = \beta _0 + \beta x _i + \epsilon _i$`

`$Y \sim N(0,\sigma^2)$`,

а значит `$\epsilon _i \sim N(0,\sigma^2)$`

т.е. можно проверить распределение остатков `$e_i$`.

- Нужно для тестов параметров, а не для подбора коэффициентов
- Нарушение не страшно --- тесты устойчивы к небольшим отклонениям
- Проверяем на квантильном графике остатков

]
.pull-right[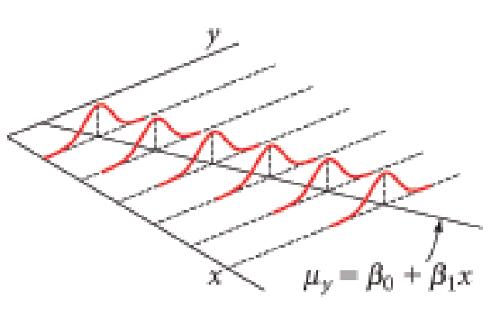

![](images/normality-assumption.png)

]

---

## 4. Гомогенность дисперсий

Нужно, т.к.

`$Y _i = \beta _0 + \beta x _i + \epsilon _i$`

`$Y \sim N(0,\sigma^2)$`

`$\sigma^2 _1 = \sigma^2 _2 = ... = \sigma^2 _i$` для каждого `$Y _i$`

Но, поскольку `$\epsilon _i \sim N(0,\sigma^2)$`, можно проверить равенство дисперсий остатков `$e_i$`

- Нужно и важно для тестов параметров
- Проверяем на графике остатков по отношению к предсказанным значениям
- Формальные тесты слишком чувствительны (тест Бройша-Пагана, тест Кокрана)

]
.pull-right[

![](images/normality-assumption.png)

]

---

## Диагностика регрессии по графикам остатков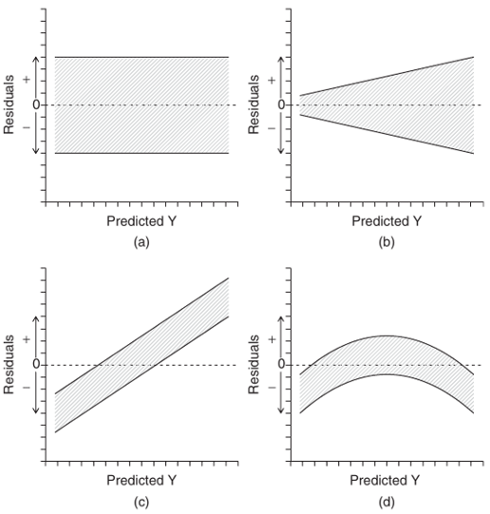

![](images/assumption-violations-on-residual-plots.png)

]
.pull-right[

- (a)все условия выполнены  
- (b)разброс остатков разный (wedge-shaped pattern)  
- (c)разброс остатков одинаковый, но нужны дополнительные предикторы  
- (d)к нелинейной зависимости применили линейную регрессию

]

---

# Ловушки при использовании <br/>корреляции и регрессии

---

## Последствия необдуманного применения <br/>линейной регрессии

[Квартет Энскомба](http://ru.wikipedia.org/wiki/Квартет_Энскомба) - примеры данных, где регрессии одинаковы во всех случаях (Anscombe, 1973)

`$y _i = 3.0 + 0.5 x _i$`

`$r^2 = 0.68$`

`$H _0: \beta _1 = 0, t = 4.24, p = 0.002$`

]
.pull-right[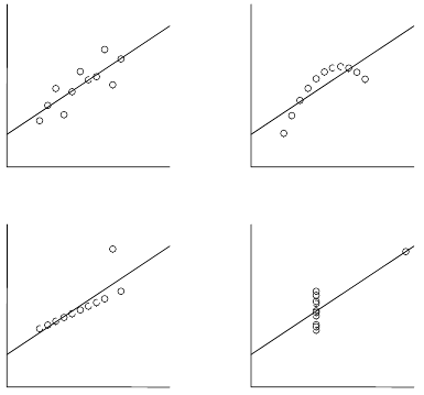

![](images/anscombe.png)

]

---

## Обратите внимание на диапазон значений

.center[
<img src="21-correlation-and-regression_files/figure-html/gg-cor-0-1.png" width="432" />
]
--

.pull-left[
<img src="21-correlation-and-regression_files/figure-html/gg-cor-1-1.png" width="468" />
]

.pull-right[
<img src="21-correlation-and-regression_files/figure-html/gg-cor-2-1.png" width="468" />
]

---

## Парадокс Симпсона

.pull-left[
<img src="21-correlation-and-regression_files/figure-html/gg-simp-1-1.png" width="468" />
]

.pull-right[
<img src="21-correlation-and-regression_files/figure-html/gg-simp-2-1.png" width="468" />

]

---

## Парадокс Симпсона

.pull-left[
<img src="21-correlation-and-regression_files/figure-html/gg-simp-4-1.png" width="468" />
]

.pull-right[
<img src="21-correlation-and-regression_files/figure-html/gg-simp-5-1.png" width="468" />

]

---

## Наличие связи между переменными <br/>не означает причинно-следственных отношений

> Correlation does not imply causation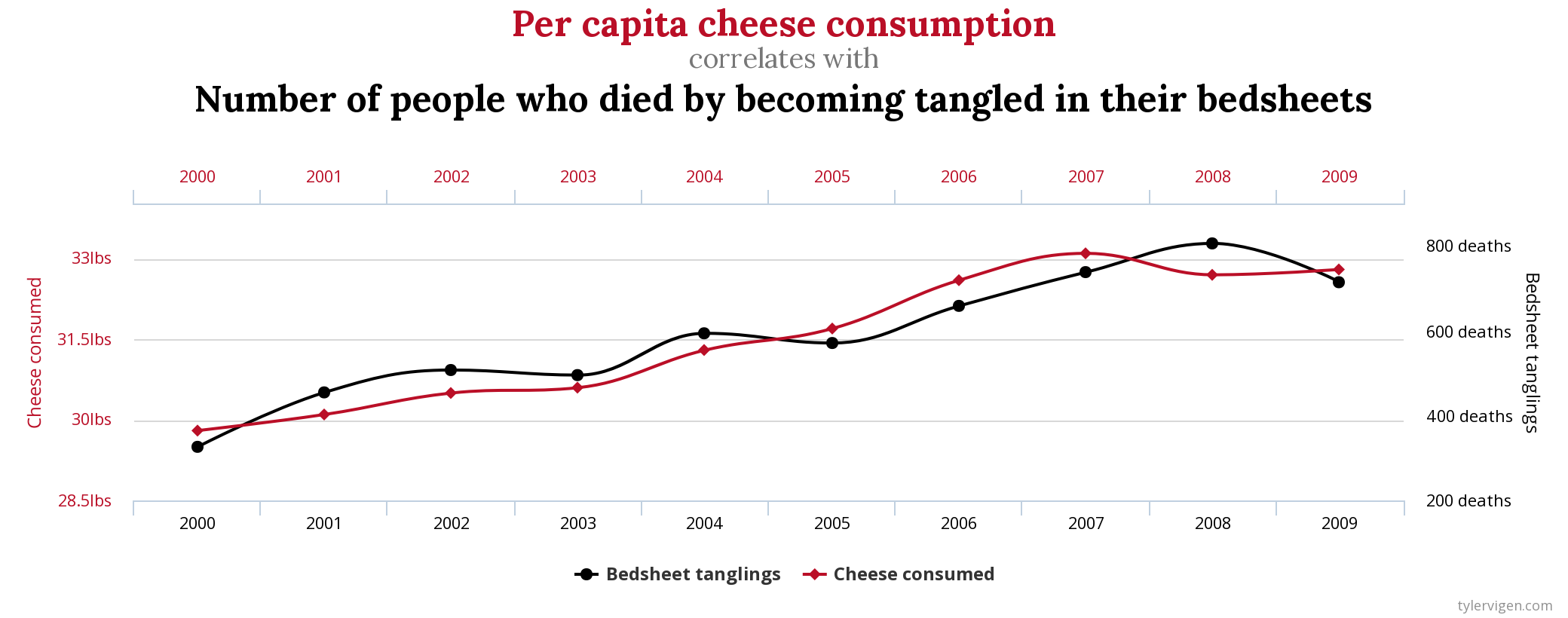

![](images/correlation-cheese-bedsheet-deaths.png)
.tiny[https://www.tylervigen.com/spurious-correlations]

---

# Summary

---

## Summary

- Коэффициент корреляции Пирсона `$r$` оценивает силу и направление связи между численными величинами (линейную составляющую)
- Корреляция не означает причинно-следственной связи между переменными.

- Условия применимости коэффициента корреляции Пирсона
  - Двумерное нормальное распределение переменных 
  - Дисперсия одной переменной не должна зависеть от другой
  - Не должно быть выбросов (= outliers)
  - Связь должна быть линейной.

- Непараметрическая альтернатива — использование коэффициентов корреляции Спирмена или Кендалла.

---

## Summary

- Модель простой линейной регрессии `$y _i = b _0 + b _1 x _i + e _i$`
- `$y$` называется откликом, а `$x$` — предиктором, коэффициент `$b_0$` — свободный член линейной модели кодирует отрезок, `$b_1$` — это коэффициент угла наклона. 
- Параметры модели оцениваются на основе выборки.
- В оценке коэффициентов регрессии, положения регрессионной прямой и предсказанных значений существует неопределенность.
- Доверительные интервалы (двух сортов) можно рассчитать, зная стандартные ошибки.

- Гипотезы о наличии взаимосвязи между откликом и предиктором можно тестировать при помощи t- или F-теста.
- Качество подгонки модели можно оценить при помощи коэффициента детерминации `$R^2$`.

---

## Summary

- Условия применимости линейных моделей
  - Независимость наблюдений
  - Линейность связи
  - Нормальное распределение остатков
  - Равенство дисперсий остатков

- Если условия применимости нарушены, то результатам тестов для этой модели нельзя верить (получаются заниженные доверительные вероятности, возрастает вероятность ошибок I рода).
- Анализ остатков дает разностороннюю информацию о валидности моделей.

---

## Что почитать

+ Гланц, С., 1998. Медико-биологическая статистика. М., Практика
+ Кабаков Р.И. R в действии. Анализ и визуализация данных на языке R. М.: ДМК Пресс, 2014
+ Diez, D.M., Barr, C.D. and Çetinkaya-Rundel, M., 2015. OpenIntro Statistics. OpenIntro.
+ Zuur, A., Ieno, E.N. and Smith, G.M., 2007. Analyzing ecological data. Springer Science & Business Media.
+ Quinn G.P., Keough M.J. 2002. Experimental design and data analysis for biologists
+ Logan M. 2010. Biostatistical Design and Analysis Using R. A Practical Guide