class: middle, left, inverse, title-slide .title[ # Обобщенные линейные модели с Пуассоновским распределением остатков ] .subtitle[ ## Линейные модели… ] .author[ ### Марина Варфоломеева, Вадим Хайтов ] .date[ ### Осень 2022 ] --- ## Мы рассмотрим + Варианты анализа для случаев, когда зависимая перменная --- счетная величина (целые неотрицательные числа) ### Вы сможете + Объяснить особенности разных типов распределений, принадлежащих экспоненциальному семейству. + Построить пуасоновскую и квази-пуассоновскую линейную модель + Объяснить проблемы, связанные с избыточностью дисперсии в модели + Построить модель, основанную на отрицательном биномиальном распределении --- ## Распределение Пуассона .pull-left[ <!-- --> ] .pull-right[ `$$f(y)= \frac{\mu^y \cdot e^{-\mu}}{y!}$$` Параметр: - `\(\mu\)` -- задает среднее и дисперсию <br/> Свойства: - `\(E(y) = \mu\)` --- мат.ожидание - `\(var(y) = \mu\)` --- дисперсия - `\(0 \le y \le +\infty\)`, `\(y \in \mathbb{N}\)` --- значения ] --- ## Отрицательное биномиальное распределение .pull-left[ <!-- --> ] .pull-right[ `\(f(y) = \frac{\Gamma(y + k)}{\Gamma(k) \cdot \Gamma(y+1)} \cdot (\frac{k}{\mu + k})^k \cdot (1 - \frac{k}{\mu + k})^y\)` Параметры: - `\(\mu\)` -- среднее - `\(k\)` -- определяет степень избыточности дисперсии <br/> Свойства: - `\(E(y) = \mu\)` -- мат.ожидание - `\(var(y) = \mu + \frac {\mu^2}{k}\)` -- дисперсия - `\(0 \le y \le +\infty\)`, `\(y \in \mathbb{N}\)` -- значения ] ??? Это смесь Пуассоновского и Гамма распределений: `\(y\)` подчиняется распределению Пуассона с Гамма-распределенным `\(\mu\)`. Приближается к распр. Пуассона при очень больших `\(k\)`. --- ## GLM в "туннеле" из распределений В каждом конкретном случае при анализе данных нам предстоит выяснить, какое из распределений больше подходит для моделирования отклика. - Достаточно ли возможностей распределения Пуассона, чтобы описать связь среднего и дисперсии? - Если нет, то справится ли отрицательное биномиальное распределениие, у которого есть параметр, для описания этой связи? <!-- --> --- background-image: url("images/Muscari_comosum_flowers.jpeg") background-position: center background-size: cover # Пример: визиты опылителей --- class: split-two .row.bg-main1[.content[ ## Мускари, копеечник и визиты опылителей Мускари (_Leopoldia comosa_) --- представитель родной флоры острова Менорка. В 18-19вв на остров завезли копеечник венечный (_Hedysarum coronarium_), который быстро натурализовался. Оба вида цветут одновременно и опыляются насекомыми. Как зависит число визитов опылителей на цветки мускари от присутствия вселенца и разнообразия флоры в ближайшей окрестности? (Данные Montero-Castaño, Vilà, 2015) ]] .row.bg-main2[ .split-three[ .column[ .center[  .tiny[Muscari à toupet (Muscari comosum), Dordogne, France --- Père Igor] ] ] .column[ .center[  ] ] .column[ .center[  .tiny[French-honeysuckle. Close to Santadi Basso, Sardinia, Italy --- Hans Hillewaert] ] ]]] ??? https://doi.org/10.1371/journal.pone.0128595 --- ## Дизайн исследования Подсчитывали число визитов опылителей на выбранное растение мускари <br/> (в пунктирной рамке) на трех типах участков. <img src="images/journal.pone.0128595.g002.PNG" width="600px" /> .left-column[ <img src="images/bee-positive.png" width="100px" /> ] .right-column[.right[.small[Fig.2 из [Montero-Castaño, Vilà, 2015](https://doi.org/10.1371/journal.pone.0128595)]]] --- ## Переменные Отклик и главный предиктор: - `Visits` --- число визитов всех опылителей на цветок мускари - `Treatment` --- тип площадки, тритмент (фактор с 3 уровнями): - `Invaded` --- мускари в смеси с видом-вселенцем; - `Removal` --- мускари в смеси с видом-вселенцем с удаленными цветками; - `Control` --- мускари без вида-вселенца. -- Важные ковариаты: - `DiversityD_1` --- Разнообразие флоры на площадке ( `\(exp(H’)\)`, где `\(H'\)` --- индекс Шеннона-Уивера) (возможно, на луг с более разнообразной растительностью прилетит больше опылителей). - `Flowers` --- число цветков мускари на площадке (чем больше, тем больше опылителей). - `Hours` --- продолжительность наблюдений (чем дольше, тем больше насчитали). -- Другие переменные: - `Total_1` --- общая плотность цветков - `Visits_NO_Apis` --- посещения опылителей без учета пчел - `Fruit` --- число цветов с плодами через месяц - `No_Fruit` --- число цветов без плодов через месяц --- ## Открываем из знакомимся с данными ```r library(readxl) pol <- read_excel("data/Pollinators_Montero-Castano, Vila, 2015.xlsx", sheet = 1) head(pol) ``` ``` # A tibble: 6 × 10 Individual Treatment DiversityD_1 Visits Visits…¹ Total_1 Fruit No_Fr…² Flowers Hours <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 1 Removal 2.66 4 4 53.9 0 10 22 0.75 2 2 Removal 1 6 6 2.45 2 7 25 0.75 3 3 Removal 1.44 5 5 41.6 5 14 40 0.75 4 4 Removal 2.21 1 1 58.8 6 9 39 0.75 5 5 Removal 2.83 6 6 19.6 3 13 45 0.75 6 6 Removal 2.40 2 2 78.4 1 21 60 0.75 # … with abbreviated variable names ¹​Visits_NO_Apis, ²​No_Fruit ``` -- ```r # Сколько пропущенных значений? colSums(is.na(pol)) ``` ``` Individual Treatment DiversityD_1 Visits Visits_NO_Apis 0 0 0 0 0 Total_1 Fruit No_Fruit Flowers Hours 0 0 0 0 0 ``` --- ## Есть ли выбросы? ```r library(ggplot2) theme_set(theme_bw()) ``` ```r library(cowplot) dot_plot <- ggplot(pol, aes(y = 1:nrow(pol))) + geom_point() plot_grid(dot_plot + aes(x = DiversityD_1), dot_plot + aes(x = Flowers), dot_plot + aes(x = Hours), nrow = 1) ``` <!-- --> -- - Выбросов нет. - Разную продолжительность периодов наблюдений нужно учесть в модели. --- ## Каков объем выборки? ```r table(pol$Treatment) ``` ``` Control Invaded Removal 14 11 18 ``` -- ### Как распределены короткие периоды наблюдений по тритментам? ```r table(pol$Hours, pol$Treatment) ``` ``` Control Invaded Removal 0.5 2 1 0 0.75 12 10 18 ``` --- ## Коллинеарны ли непрерывные и дискретные предикторы? ```r box_plot <- ggplot(pol, aes(x = Treatment)) + geom_boxplot() plot_grid(box_plot + aes(y = DiversityD_1), box_plot + aes(y = Flowers), nrow = 1) ``` <!-- --> -- - Возможно, есть коллинеарность. Перед подбором модели проверим это при помощи `vif()` --- ## Как распределена переменная-отклик? Число визитов насекомых -- счетная переменная. Для ее моделирования нужно использовать подходящее распределение. ```r ggplot(pol, aes(x = Visits)) + geom_histogram() ``` 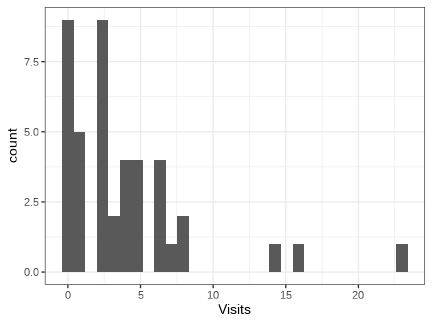<!-- --> ```r mean(pol$Visits == 0) # Какова пропорция нулей? ``` ``` [1] 0.2093 ``` - Примерно 21% наблюдений -- нули. Иногда из-за избытка нулей (Zero inflation) в модели может появиться избыточность дисперсии. Будем иметь это в виду. --- class: middle, center, inverse # GLM с нормальным распределением отклика --- ## Что будет, если проигнорировать, что отклик --- численная переменная? -- `\(Visits_i \sim N(\mu_i, \sigma)\)` -- `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = \sigma^2\)` -- `\(\mu_i = \eta_i\)` -- функция связи "идентичность" -- `\(\eta_i = b_0 + b_1 Treatment_{Invaded\ i} + b_2 Treatment_{Removal\ i} + \\ + b_3 DiversityD1_{i} + b_4 Flowers_{i} + b_5 Hours_{i}\)` -- ```r M_norm <- glm(Visits ~ Treatment + DiversityD_1 + Flowers + Hours, data = pol) coef(M_norm) ``` ``` (Intercept) TreatmentInvaded TreatmentRemoval -3.2545 2.8908 -1.0617 DiversityD_1 Flowers Hours -1.2041 0.1439 6.6546 ``` ```r sigma(M_norm) ``` ``` [1] 4.174 ``` -- `\(Visits_i \sim N(\mu_i, 4.17)\)` `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = \sigma^2\)` `\(\mu_i = \eta_i\)` `\(\eta_i = -3.3 + 2.9 Treatment_{Invaded\ i} -1.1 Treatment_{Removal\ i} - \\ -1.2 DiversityD1_{i} + 0.1 Flowers_{i} + 6.7 Hours_{i}\)` --- ## Данные для графика предсказаний простой линейной модели ```r library(dplyr) NewData <- pol %>% group_by(Treatment)%>% do(data.frame(Flowers = seq(min(.$Flowers), max(.$Flowers), length.out=50))) %>% mutate(DiversityD_1 = mean(pol$DiversityD_1), Hours = 0.75) # Модельная матрица и коэффициенты X <- model.matrix(~ Treatment + DiversityD_1 + Flowers + Hours, data = NewData) betas <- coef(M_norm) # Предсказания в масштабе функции связи (eta) уже в масштабе отклика (mu) NewData$mu <- X %*% betas NewData$SE_mu <- sqrt(diag(X %*% vcov(M_norm) %*% t(X))) # SE head(NewData, 3) ``` ``` # A tibble: 3 × 6 # Groups: Treatment [1] Treatment Flowers DiversityD_1 Hours mu[,1] SE_mu <chr> <dbl> <dbl> <dbl> <dbl> <dbl> 1 Control 11 1.86 0.75 1.08 1.54 2 Control 11.7 1.86 0.75 1.18 1.52 3 Control 12.4 1.86 0.75 1.28 1.49 ``` --- ## График предсказаний ```r ggplot(NewData, aes(x = Flowers, y = mu, fill = Treatment)) + geom_ribbon(aes(ymin = mu - 2 * SE_mu, ymax = mu + 2 * SE_mu), alpha=0.3)+ geom_line(aes(colour = Treatment)) + geom_hline(yintercept = 0) ``` .pull-left[ <!-- --> ] -- .pull-right[ .center[  Отрицательные предсказания! ] ] -- С такой моделью работать точно нельзя, но мы продолжим из любопытства. Нужно же посмотреть, какие еще проблемы возникают при использовании нормального распределения для моделирования счетных величнн. --- ## Результаты подбора модели ```r summary(M_norm) ``` ``` Call: glm(formula = Visits ~ Treatment + DiversityD_1 + Flowers + Hours, data = pol) Deviance Residuals: Min 1Q Median 3Q Max -7.432 -2.361 -0.393 1.034 13.238 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -3.2545 7.7310 -0.42 0.676 TreatmentInvaded 2.8908 1.7626 1.64 0.109 TreatmentRemoval -1.0617 1.6776 -0.63 0.531 DiversityD_1 -1.2041 0.7851 -1.53 0.134 Flowers 0.1439 0.0585 2.46 0.019 * Hours 6.6546 10.6424 0.63 0.536 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for gaussian family taken to be 17.42) Null deviance: 891.86 on 42 degrees of freedom Residual deviance: 644.61 on 37 degrees of freedom AIC: 252.4 Number of Fisher Scoring iterations: 2 ``` --- ## Анализ девиансы для модели с нормальным распределением отклика ```r drop1(M_norm, test = 'Chi') ``` ``` Single term deletions Model: Visits ~ Treatment + DiversityD_1 + Flowers + Hours Df Deviance AIC scaled dev. Pr(>Chi) <none> 645 252 Treatment 2 744 255 6.17 0.046 * DiversityD_1 1 686 253 2.65 0.104 Flowers 1 750 257 6.51 0.011 * Hours 1 651 251 0.45 0.501 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` -- Число визитов опылителей на цветки мускари: - НЕ зависит от присутствия вселенца и его цветов, - НЕ зависит от разнообразия флоры на участке, - зависит от числа цветов мускари. Прежде чем доверять этим результатам, нужно проверить, выполняются ли условия применимости. --- ## Нет ли коллинеарности предикторов ```r library(car) vif(M_norm) ``` ``` GVIF Df GVIF^(1/(2*Df)) Treatment 1.357 2 1.079 DiversityD_1 1.162 1 1.078 Flowers 1.226 1 1.107 Hours 1.134 1 1.065 ``` -- - Коллинеарности нет. --- ## Задание 1 Постройте график пирсоновских остатков от предсказанных значений для модели `M_norm`. Какие нарушения условий применимости вы на нем видите? <br/> Дополните код: ```r M_norm_diag <- data.frame(.fitted = fitted(), .resid_p = residuals()) ggplot(data = , aes()) + geom_hline( = 0) + geom_point() ``` --- ## График остатков от предсказанных значений ```r M_norm_diag <- data.frame(.fitted = fitted(M_norm, type = "response"), .resid_p = residuals(M_norm, type = "pearson")) ggplot(M_norm_diag, aes(y = .resid_p)) + geom_hline(yintercept = 0) + geom_point(aes(x = .fitted)) ``` .pull-left[ <!-- --> ] -- .pull-right[ .center[  ] - Гетерогенность дисперсий остатков. - Отрицательные предсказания! ] -- Чуда не произошло --- ## Модель с нормальным распределением отклика <br/>не подходит Два способа решения проблем с моделью: 1. Грубый способ: логарифмировать зависимую переменную и построить модель для нее. 2. Лучше построить модель, основанную на распределении, подходящем для счетных данных: - распределение Пуассона, - отрицательное биномиальное распределение. --- class: middle, center, inverse # GLM с Пуассоновским распределением отклика --- ## GLM с Пуассоновским распределением отклика -- `\(Visits_i \sim Poisson(\mu_i)\)` -- `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = \mu_i\)` -- `\(\text{ln}(\mu_i) = \eta_i\)` --- функция связи логарифм -- `\(\begin{aligned}\eta_i & = b_0 + b_1 Treatment_{Invaded\ i} + b_2 Treatment_{Removal\ i} + \\ &+ b_3 DiversityD1_{i} + b_4 Flowers_{i} + b_5 Hours_{i}\end{aligned}\)` -- ```r M_pois <- glm(Visits ~ Treatment + DiversityD_1 + Flowers + Hours, data = pol, family = "poisson") coef(M_pois) ``` ``` (Intercept) TreatmentInvaded TreatmentRemoval -2.66091 0.71342 -0.21538 DiversityD_1 Flowers Hours -0.45740 0.03731 4.68669 ``` -- `\(Visits_i \sim Poisson(\mu_i)\)` `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = \mu_i\)` `\(\text{ln}(\mu_i) = \eta_i\)` `\(\begin{aligned}\eta_i = &-2.66 + 0.71 Treatment_{Invaded\ i} - 0.22 Treatment_{Removal\ i} - \\ &- 0.46 DiversityD1_i + 0.04 Flowers_i + 4.69 Hours_i\end{aligned}\)` --- ## Тесты коэффициентов Пуассоновской GLM .left-column[ .small[Для тестирования значимости коэффициентов в Пуассоновской GLM используются __z-тесты Вальда__, т.к. не приходится оценивать дисперсию и t-статистика Вальда будет подчиняться нормальному распределению. ] ] .right-column[ ```r summary(M_pois) ``` ``` Call: glm(formula = Visits ~ Treatment + DiversityD_1 + Flowers + Hours, family = "poisson", data = pol) Deviance Residuals: Min 1Q Median 3Q Max -4.067 -1.319 -0.352 0.707 3.235 Coefficients: Estimate Std. Error z value Pr(>|z|) *(Intercept) -2.66091 2.17444 -1.22 0.22106 TreatmentInvaded 0.71342 0.21416 3.33 0.00086 *** TreatmentRemoval -0.21538 0.22265 -0.97 0.33337 DiversityD_1 -0.45740 0.12859 -3.56 0.00037 *** Flowers 0.03731 0.00683 5.46 0.000000048 *** Hours 4.68669 2.90325 1.61 0.10646 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 189.75 on 42 degrees of freedom Residual deviance: 119.88 on 37 degrees of freedom AIC: 238.8 Number of Fisher Scoring iterations: 6 ``` ] --- ## Смысл коэффициентов Пуассоновской GLM .left-column[ .small[__Интерсепт__ `\(b_0\)` показывает чему равно значение `\(\eta = ln(\mu_i)\)` на базовом уровне, когда все предикторы `\(x_k = 0\)`. Значит, значение самого отклика равно `\(e^{b_0}\)`.] .small[Т.е. если разнообразие цветов DiversityD_1, обилие цветов Flowers и время наблюдения Hours равны нулю, то ожидаемое число визитов опылителей `\(e^{-2.661} = 0.07\)`. Для этих данных `\(b_0\)` не имеет биологического смысла. ] ] .right-column[ ```r summary(M_pois) ``` ``` Call: glm(formula = Visits ~ Treatment + DiversityD_1 + Flowers + Hours, family = "poisson", data = pol) Deviance Residuals: Min 1Q Median 3Q Max -4.067 -1.319 -0.352 0.707 3.235 Coefficients: Estimate Std. Error z value Pr(>|z|) *(Intercept) -2.66091 2.17444 -1.22 0.22106 TreatmentInvaded 0.71342 0.21416 3.33 0.00086 *** TreatmentRemoval -0.21538 0.22265 -0.97 0.33337 DiversityD_1 -0.45740 0.12859 -3.56 0.00037 *** Flowers 0.03731 0.00683 5.46 0.000000048 *** Hours 4.68669 2.90325 1.61 0.10646 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 189.75 on 42 degrees of freedom Residual deviance: 119.88 on 37 degrees of freedom AIC: 238.8 Number of Fisher Scoring iterations: 6 ``` ] --- ## Смысл коэффициентов Пуассоновской GLM .left-column[ .small[Коэффициенты `\(b_k\)` при переменных-индикаторах `\(x_k\)`, кодирующих уровни __дискретных предикторов__, показывают, на сколько единиц отличается значение `\(\eta = ln(\mu_i)\)` от базового уровня. Значит, значение отклика отличается в `\(e^{b_k}\)` раз от базового уровня.] .small[Т.е. в присутствии вида-вселенца в `\(e^{0.713} = 2.04\)` раза больше визитов опылителей, а при удалении - в `\(e^{-0.215} = 0.81\)` раза, т.е. на 19% меньше чем в контроле. ] ] .right-column[ ```r summary(M_pois) ``` ``` Call: glm(formula = Visits ~ Treatment + DiversityD_1 + Flowers + Hours, family = "poisson", data = pol) Deviance Residuals: Min 1Q Median 3Q Max -4.067 -1.319 -0.352 0.707 3.235 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.66091 2.17444 -1.22 0.22106 *TreatmentInvaded 0.71342 0.21416 3.33 0.00086 *** *TreatmentRemoval -0.21538 0.22265 -0.97 0.33337 DiversityD_1 -0.45740 0.12859 -3.56 0.00037 *** Flowers 0.03731 0.00683 5.46 0.000000048 *** Hours 4.68669 2.90325 1.61 0.10646 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 189.75 on 42 degrees of freedom Residual deviance: 119.88 on 37 degrees of freedom AIC: 238.8 Number of Fisher Scoring iterations: 6 ``` ] --- ## Смысл коэффициентов Пуассоновской GLM .left-column[ .small[Угловые коэффициенты при __непрерывных предикторах__ `\(b_k\)` показывают, на сколько единиц меняется значение `\(\eta = ln(\mu_i)\)`, если предиктор `\(x_k\)` изменяется на единицу. Значит, сам отклик изменяется в `\(e^{b_k}\)` раз.] .small[Т.е. при росте биоразнообразия на 1 число визитов изменяется в `\(e^{-0.457} = 0.63\)` раз, т.е. уменьшается на 37%. А если цветков мускари больше на 1, то растет в `\(e^{0.037} = 1.04\)` раз, т.е. на 4%. ] ] .right-column[ ```r summary(M_pois) ``` ``` Call: glm(formula = Visits ~ Treatment + DiversityD_1 + Flowers + Hours, family = "poisson", data = pol) Deviance Residuals: Min 1Q Median 3Q Max -4.067 -1.319 -0.352 0.707 3.235 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.66091 2.17444 -1.22 0.22106 TreatmentInvaded 0.71342 0.21416 3.33 0.00086 *** TreatmentRemoval -0.21538 0.22265 -0.97 0.33337 *DiversityD_1 -0.45740 0.12859 -3.56 0.00037 *** *Flowers 0.03731 0.00683 5.46 0.000000048 *** *Hours 4.68669 2.90325 1.61 0.10646 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 189.75 on 42 degrees of freedom Residual deviance: 119.88 on 37 degrees of freedom AIC: 238.8 Number of Fisher Scoring iterations: 6 ``` ] --- ## Анализ девиансы для модели с Пуассоновским распределением отклика ```r drop1(M_pois, test = 'Chi') ``` ``` Single term deletions Model: Visits ~ Treatment + DiversityD_1 + Flowers + Hours Df Deviance AIC LRT Pr(>Chi) <none> 120 239 Treatment 2 145 260 25.41 0.000003037 *** DiversityD_1 1 134 251 14.43 0.00015 *** Flowers 1 149 266 28.79 0.000000081 *** Hours 1 124 240 3.76 0.05261 . --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` -- Число визитов опылителей на цветки мускари: - зависит от присутствия вида-вселенца и его цветов, - зависит от разнообразия флоры на данном участке, - зависит от числа цветов самого мускари. Можем ли мы доверять этим результатам? Пока не известно. --- ## Данные для предсказаний ```r NewData <- pol %>% group_by(Treatment)%>% do(data.frame(Flowers = seq(min(.$Flowers), max(.$Flowers), length.out=50))) %>% mutate(DiversityD_1 = mean(pol$DiversityD_1), Hours = 0.75) ``` Давайте получим предсказания при помощи операций с матрицами, чтобы своими глазами увидеть работу функции связи. .pull-down[.content-box-red[ Осторожно! Хоть и можно получить предсказания при помощи `predict()`, но **`predict()` возвращает "правильные" `SE` только в масштабе функции связи!** ```r ?predict.glm ``` <br/> ]] --- ## Задание 2 Дополните код, чтобы получить предсказания модели при помощи операций с матрицами. ```r # Модельная матрица и коэффициенты X <- betas <- # Предсказанные значения и стандартные ошибки... # ...в масштабе функции связи (логарифм) NewData$fit_eta <- NewData$SE_eta <- sqrt(( %*% vcov(M_pois) %*% )) # ...в масштабе отклика (применяем функцию, обратную функции связи) NewData$fit_mu <- NewData$lwr <- NewData$upr <- ``` --- ## Предсказания модели при помощи операций с матрицами ```r # Модельная матрица и коэффициенты X <- model.matrix(~ Treatment + DiversityD_1 + Flowers + Hours, data = NewData) betas <- coef(M_pois) # Предсказанные значения и стандартные ошибки... # ...в масштабе функции связи (логарифм) NewData$fit_eta <- X %*% betas NewData$SE_eta <- sqrt(diag(X %*% vcov(M_pois) %*% t(X))) # ...в масштабе отклика (применяем функцию, обратную функции связи) NewData$fit_mu <- exp(NewData$fit_eta) NewData$lwr <- exp(NewData$fit_eta - 2 * NewData$SE_eta) NewData$upr <- exp(NewData$fit_eta + 2 * NewData$SE_eta) head(NewData, 2) ``` ``` # A tibble: 2 × 9 # Groups: Treatment [1] Treatment Flowers DiversityD_1 Hours fit_eta[,1] SE_eta fit_mu[,1] lwr[,1] upr[,1] <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 Control 11 1.86 0.75 0.415 0.224 1.51 0.968 2.37 2 Control 11.7 1.86 0.75 0.441 0.221 1.55 0.999 2.42 ``` --- ## График предсказаний в масштабе функции связи ```r ggplot(NewData, aes(x = Flowers, y = fit_eta, fill = Treatment)) + geom_ribbon(aes(ymin = fit_eta - 2 * SE_eta, ymax = fit_eta + 2 * SE_eta), alpha = 0.5) + geom_line(aes(colour = Treatment)) + geom_hline(yintercept = 0) ``` .pull-left[ <!-- --> ] -- .pull-right[ В масштабе функции связи мы моделируем линейную зависимость логарифмов мат. ожидания отклика от предикторов. ] --- ## График предсказаний в масштабе переменной-отклика ```r ggplot(NewData, aes(x = Flowers, y = fit_mu, fill = Treatment)) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.5) + geom_line(aes(colour = Treatment)) + geom_hline(yintercept = 0) ``` .pull-left[ <!-- --> ] -- .pull-right[  GLM с Пуассоновским распределением отклика моделирует его нелинейную cвязь предикторами за счет функции связи `\(log()\)`. И никаких отрицательных предсказаний! ] --- ## Возможные с Пуассоновской GLM GLM с Пуассоновским распределением отклика учитывает гетерогенность дисперсии, т.к. `\(var(y_i) = mu_i = E(y_i)\)`. Стандартные ошибки возрастают с увеличением предсказанного значения. .pull-left[ <!-- --> ] -- .pull-right[ Но достаточно ли этого для моделирования данных? Нет ли здесь сверхдисперсии?    ] --- ## Условия применимости GLM с Пуассоновским распределением отклика - Случайность и независимость наблюдений внутри групп. - Отсутствие сверхдисперсии. (Дисперсия остатков равна мат.ожиданию при каждом уровне значений предикторов). - Отсутствие коллинеарности предикторов. --- ## График остатков ```r M_pois_diag <- data.frame(.fitted = fitted(M_pois, type = "response"), .resid_p = residuals(M_pois, type = "pearson")) ggplot(M_pois_diag, aes(x = .fitted, y = .resid_p)) + geom_point() + geom_hline(yintercept = 0) ``` .pull-left[ 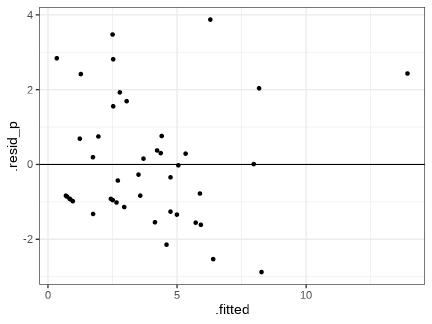<!-- --> А что это за странные полоски? ] -- .pull-right[ Полоски из точек — это наблюдения с разными значениями отклика: 0, 1, 2, ... визита опылителей. Нет никаких отрицательных предсказаний!  ] --- class: middle, center, inverse # Избыточность дисперсии (overdispersion) --- ## Избыточность дисперсии (overdispersion) Если данные подчиняются распределению Пуассона, то дисперсия должна быть равна среднему значению. - `\(E(y_i) = \mu_i\)` - `\(var(y_i) = \mu_i\)` Если это не так, то мы не сможем доверять результатам. Это будет значить, что мы применяем модель, основанную на Пуассоновском распределении, к данным, которые не подчиняются этому распределению. --- ## Если есть избыточность дисперсии... Пуассоновские модели недооценивают (приуменьшают) "раздувшиеся" стандартные ошибки. -- __В норме, если данные подчиняются распределению Пуассона__, то: `\(var(y_i) = \mu_i\)` -- Т.е. дисперсии и стандартные ошибки, "нормальные" для распределения Пуассона: `\(var(E(y_i)) = {\mu_i} / n\)` `\(SE_{E(y_i)} = \sqrt {var(E(y_i))}\)` -- __Если данные НЕ подчиняются распределению Пуассона__, и дисперсия в `\(\varphi\)` раз больше среднего ( `\(\varphi > 1\)`), то: `\(var^*(y_i) = \varphi\mu_i\)` -- Тогда дисперсии должны быть больше в `\(\varphi\)` раз, а стандартные ошибки --- в `\(\sqrt {\varphi}\)` раз: `\(var^*(E(y_i)) = {\varphi\mu_i} / n\)` `\(SE^*_{E(y_i)} = \sqrt {\varphi~var(E(y_i))}\)` __Если при сверхдисперсии использовать обычное распределение Пуассона, то оценки стандартных ошибок окажутся занижены.__ ??? Fox 2016, p.431-432 В биномиальных моделях см. Dunn, Smyth, 2018, p.347 В пуассоновских моделях см. Dunn, Smyth, 2018, p.397 --- ## Проблемы из-за неучтенной избыточности дисперсии <br/>в Пуассоновских GLM - Из-за того, что оценки стандартных ошибок занижены: + Доверительные интервалы для коэффициентов заужены + Доверительная зона предсказаний модели будет заужена + Уровень значимости в тестах Вальда для коэффициентов будет занижен. - Тесты, основанные на сравнении правдоподобий, дадут смещённые результаты, т.к. соотношение девианс не будет подчиняться `\(\chi^2\)`-распределению. --- ## Проверка на сверхдисперсию ```r # Функция для проверки наличия сверхдисперсии в модели (автор Ben Bolker) # http://bbolker.github.io/mixedmodels-misc/glmmFAQ.html # Код модифицирован, чтобы учесть дополнительный параметр в NegBin GLMM, # подобранных MASS::glm.nb() overdisp_fun <- function(model) { rdf <- df.residual(model) # Число степеней свободы N - p if (any(class(model) == 'negbin')) rdf <- rdf - 1 ## учитываем k в NegBin GLMM rp <- residuals(model,type='pearson') # Пирсоновские остатки Pearson.chisq <- sum(rp^2) # Сумма квадратов остатков, подчиняется Хи-квадрат распределению prat <- Pearson.chisq/rdf # Отношение суммы квадратов остатков к числу степеней свободы pval <- pchisq(Pearson.chisq, df=rdf, lower.tail=FALSE) # Уровень значимости c(chisq=Pearson.chisq,ratio=prat,rdf=rdf,p=pval) # Вывод результатов } ``` Модифицировано по Ben Bolker's [glmmFAQ](http://bbolker.github.io/mixedmodels-misc/glmmFAQ.html) <br/> ```r overdisp_fun(M_pois) ``` ``` chisq ratio rdf p 1.116e+02 3.016e+00 3.700e+01 2.079e-09 ``` Избыточность дисперсии есть! Дисперсия в 3 раза выше среднего. --- ## Причины избыточности дисперсии + Наличие выбросов. + В модель не включен важный предиктор или взаимодействие предикторов. + Нарушена независимость выборок (есть внутригрупповые корреляции). + Нелинейная связь между ковариатами и зависимой переменной. + Выбрана неподходящая связывающая функция. + Количество нулей больше, чем предсказывает выбранное <br/> распределение отклика (Zero inflation) . + Выбрана неподходящая функция распределения для отклика. -- ### Как бороться с избыточностью дисперсии Взвесив все, что известно о данных, можно решить, как именно усовершенствовать модель. <br/> Для модели числа визитов опылителей мы попробуем два варианта действий: - Можно построить квази-пуассоновскую модель. - Можно построить модель, основанную на отрицательном биномиальном распределении. --- class: middle, center, inverse # Квази-пуассоновские модели --- ## Квази-пуассоновские модели .left-column[ Помните, не бывает "квази-пуассоновского распределения"!  ] .right-column[ `\(Visits_i \sim Quasipoisson(\mu_i)\)` `\(E(Visits_i) = \mu_i\)`, `\(var(y_i) = \varphi\ \mu_i\)` `\(\text{ln}(\mu_i) = \eta_i\)` --- функция связи логарифм `\(\begin{aligned}\eta_i & = b_0 + b_1 Treatment_{Invaded\ i} + b_2 Treatment_{Removal\ i} + \\ &+ b_3 DiversityD1_{i} + b_4 Flowers_{i} + b_5 Hours_{i}\end{aligned}\)` <br/> Квазипуассоновские модели используют распределение Пуассона, но при этом вносится поправка для стандартных ошибок на степень избыточности дисперсии `\(\varphi\)`. `\(\varphi\)` оценивается по данным и показывает, во сколько раз дисперсия больше среднего. ] ??? Вот такой вариант оценки используется в R (рекомендован McCullagh, Nelder, 1989): `$$\varphi = \frac{var(E(y_i))}{\mu_i}=\frac {\frac{\sum{(e_{p~i})^2}}{n - p}} {\mu_i} = \frac{\sum{(e_{p~i})^2}}{n - p}$$` --- ## Особенности квази-пуассоновской GLM - Оценки параметров `\(\beta\)` такие же как в Пуассоновской GLM. - Стандартные ошибки оценок коэффициентов домножены на `\(\sqrt{\varphi}\)`. - Доверительные интервалы к оценкам коэффициентов домножены на `\(\sqrt{\varphi}\)`. - Логарифмы правдоподобий уменьшаются в `\(\varphi\)` раз. -- ### Работа с квази-моделями 1. В тестах параметров используются `\(t\)`-тесты Вальда (и `\(t\)`-распределение) вместо `\(z\)`-тестов Вальда (и стандартного нормального распределения). 2. Для анализа девиансы используются `\(F\)`-тесты. 3. Для квази-пуассоновских моделей не определена функция максимального правдоподобия, поэтому нельзя вычислить AIC (но иногда считают квази-AIC = QAIC). ??? См. Højsgaard and Halekoh 2005. Overdispersion Søren Højsgaard and Ulrich Halekoh; Biometry Research Unit Danish Institute of Agricultural Sciences; June 1, 2005 Printed: June 1, 2005 File: overdispersion http://genetics.agrsci.dk/statistics/courses/phd05/material/src/overdispersion --- ## Квази-пуассоновская модель `\(Visits_i \sim Quasipoisson(\mu_i)\)` `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = \varphi\ \mu_i\)` `\(\text{ln}(\mu_i) = \eta_i\)` --- функция связи логарифм `\(\begin{aligned}\eta_i & = b_0 + b_1 Treatment_{Invaded\ i} + b_2 Treatment_{Removal\ i} + \\ &+ b_3 DiversityD1_{i} + b_4 Flowers_{i} + b_5 Hours_{i}\end{aligned}\)` -- ```r M_quasi <- glm(Visits ~ Treatment + DiversityD_1 + Flowers + Hours, data = pol, family = "quasipoisson") coef(M_quasi) ``` ``` (Intercept) TreatmentInvaded TreatmentRemoval DiversityD_1 Flowers -2.66091 0.71342 -0.21538 -0.45740 0.03731 Hours 4.68669 ``` ```r summary(M_quasi)$dispersion ``` ``` [1] 3.016 ``` -- `\(Visits_i \sim Quasipoisson(\mu_i)\)` `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = 3.016\ \mu_i\)` `\(\text{ln}(\mu_i) = \eta_i\)` `\(\begin{aligned}\eta_i = &-2.66 + 0.71 Treatment_{Invaded\ i} - 0.22 Treatment_{Removal\ i} - \\ &- 0.46 DiversityD1_i + 0.04 Flowers_i + 4.69 Hours_i\end{aligned}\)` --- ## Результаты подбора модели Те же коэффициенты, что в Пуассоновской модели, но стандартные ошибки домножены на `\(\sqrt{\varphi}\)`. Для тестирования используются t-тесты Вальда, т.к. пришлось оценить `\(\varphi\)` и статистика Вальда больше не подчиняется нормальному распределению. ```r summary(M_quasi) ``` ``` Call: glm(formula = Visits ~ Treatment + DiversityD_1 + Flowers + Hours, family = "quasipoisson", data = pol) Deviance Residuals: Min 1Q Median 3Q Max -4.067 -1.319 -0.352 0.707 3.235 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -2.6609 3.7761 -0.70 0.4854 TreatmentInvaded 0.7134 0.3719 1.92 0.0628 . TreatmentRemoval -0.2154 0.3867 -0.56 0.5809 DiversityD_1 -0.4574 0.2233 -2.05 0.0477 * Flowers 0.0373 0.0119 3.14 0.0033 ** Hours 4.6867 5.0418 0.93 0.3586 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for quasipoisson family taken to be 3.016) Null deviance: 189.75 on 42 degrees of freedom Residual deviance: 119.88 on 37 degrees of freedom AIC: NA Number of Fisher Scoring iterations: 6 ``` --- ## Анализ девиансы для квази-пуассоновской модели ```r drop1(M_quasi, test = "F") ``` ``` Single term deletions Model: Visits ~ Treatment + DiversityD_1 + Flowers + Hours Df Deviance F value Pr(>F) <none> 120 Treatment 2 145 3.92 0.0285 * DiversityD_1 1 134 4.45 0.0417 * Flowers 1 149 8.88 0.0051 ** Hours 1 124 1.16 0.2886 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` -- Число визитов опылителей на цветки мускари: - зависит от присутствия вида-вселенца и его цветов, - зависит от разнообразия флоры на данном участке, - зависит от числа цветов самого мускари. Можем ли мы доверять этим результатам? Это приблизительные результаты. Не стоит доверять `\(p\)` близким к `\(\alpha = 0.05\)`. Из-за сверхдисперсии значимыми могут оказаться незначимые эффекты. --- class: middle, center, inverse # GLM с отрицательным биномиальным распределением отклика --- ### GLM с отрицательным биномиальным распределением -- `\(Visits_i \sim NB(\mu_i, k)\)` -- `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = \mu_i + \frac{\mu_i^2}{k}\)` -- `\(\text{ln}(\mu_i) = \eta_i\)` --- функция связи логарифм -- `\(\eta = b_0 + b_1 Treatment_{Invaded\ i} + b_2 Treatment_{Removal\ i} + \\ + b_3 DiversityD1_{i} + b_4 Flowers_{i} + b_5 Hours_{i}\)` -- ```r library(MASS) M_nb <- glm.nb(Visits ~ Treatment + DiversityD_1 + Flowers + Hours, data = pol, link = "log") coef(M_nb) ``` ``` (Intercept) TreatmentInvaded TreatmentRemoval -1.97122 0.56873 -0.10896 DiversityD_1 Flowers Hours -0.48868 0.03093 4.10246 ``` ```r summary(M_nb)$theta ``` ``` [1] 1.936 ``` -- .small[ `\(Visits_i \sim NB(\mu_i, 1.936)\)` `\(E(Visits_i) = \mu_i\)`, `\(var(Visits_i) = \mu_i + \frac{\mu_i^2}{1.936}\)` `\(\text{ln}(\mu_i) = \eta_i\)` `\(\eta_i = -1.97 + 0.57 Treatment_{Invaded\ i} - 0.11 Treatment_{Removal\ i} -\\ -0.49 DiversityD1_{i} + 0.03 Flowers_{i} + 4.10 Hours_{i}\)` ] --- ## Результаты подбора модели Коэффициенты отличаются от Пуассоновской модели, но интерпретируются аналогично. Для тестирования используются z-тесты Вальда, т.к. статистика Вальда подчиняется нормальному распределению. ```r summary(M_nb) ``` ``` Call: glm.nb(formula = Visits ~ Treatment + DiversityD_1 + Flowers + Hours, data = pol, link = "log", init.theta = 1.935929584) Deviance Residuals: Min 1Q Median 3Q Max -2.460 -0.972 -0.244 0.471 1.544 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -1.9712 2.4530 -0.80 0.422 TreatmentInvaded 0.5687 0.3882 1.46 0.143 TreatmentRemoval -0.1090 0.3769 -0.29 0.773 DiversityD_1 -0.4887 0.1990 -2.46 0.014 * Flowers 0.0309 0.0128 2.42 0.016 * Hours 4.1025 3.2949 1.25 0.213 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for Negative Binomial(1.936) family taken to be 1) Null deviance: 70.826 on 42 degrees of freedom Residual deviance: 48.891 on 37 degrees of freedom AIC: 208.8 Number of Fisher Scoring iterations: 1 Theta: 1.936 Std. Err.: 0.723 2 x log-likelihood: -194.849 ``` --- ## Анализ девиансы модели с отрицательным биномиальным распределением отклика ```r drop1(M_nb, test = 'Chi') ``` ``` Single term deletions Model: Visits ~ Treatment + DiversityD_1 + Flowers + Hours Df Deviance AIC LRT Pr(>Chi) <none> 48.9 207 Treatment 2 53.4 207 4.50 0.106 DiversityD_1 1 54.7 211 5.84 0.016 * Flowers 1 55.4 211 6.51 0.011 * Hours 1 50.4 206 1.49 0.222 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ``` -- Число визитов опылителей на цветки мускари: - не зависит от присутствия вида-вселенца и его цветов, - зависит от разнообразия флоры на данном участке, - зависит от числа цветов самого мускари. Можем ли мы доверять этим результатам? Это нужно еще проверить. --- ## Задание 3 Проведите диагностику модели `M_nb`. Видите ли вы какие-нибудь нарушения условий применимости? --- ## График остатков ```r M_nb_diag <- data.frame(.fitted = fitted(M_nb, type = "response"), .resid_p = residuals(M_nb, type = "pearson"), pol) gg_resid <- ggplot(M_nb_diag, aes(y = .resid_p)) + geom_hline(yintercept = 0) gg_resid + geom_point(aes(x = .fitted)) ``` <!-- --> -- Ничего необычного (нет отрицательных предсказаний, нет заметной нелинейности). --- ## Проверка на сверхдисперсию Обратите внимание, у моделей с отрицательным биномиальным распределением добавляется еще один параметр ```r overdisp_fun(M_nb) ``` ``` chisq ratio rdf p 38.9817 1.0828 36.0000 0.3371 ``` -- Избыточности дисперсии нет --- ## Графики остатков от переменных, которые есть в модели ```r plot_grid(gg_resid + geom_boxplot(aes(x = Treatment)), gg_resid + geom_boxplot(aes(x = as.factor(Hours))), gg_resid + geom_point(aes(x = DiversityD_1)), gg_resid + geom_point(aes(x = Flowers)), nrow = 2) ``` .pull-left[ <!-- --> ] .pull-right[ Ничего страшного. Может показаться, что есть какой-то невнятный нелинейный паттерн на графике зависимости отстатков от количества цветков мускари, но скорее всего это связано с небольшим количеством наблюдений. ] --- ## Графики остатков от переменных, которых нет в модели Из всех оставшихся переменных только `Total_1` можно рассматривать как потенциальный предиктор. ```r gg_resid + geom_point(aes(x = Total_1)) ``` <!-- --> -- Ничего криминального. Никаких паттернов. Можно не включать в модель. --- ## Данные для предсказаний ```r NewData <- pol %>% group_by(Treatment)%>% do(data.frame(Flowers = seq(min(.$Flowers), max(.$Flowers), length.out=50))) %>% mutate(DiversityD_1 = mean(pol$DiversityD_1), Hours = 0.75) ``` Как и в прошлый раз, давайте получим предсказания при помощи операций с матрицами, чтобы своими глазами увидеть работу функции связи. .pull-down[.content-box-red[ Осторожно! Хоть и можно получить предсказания при помощи `predict()`, но **`predict()` возвращает "правильные" `SE` только в масштабе функции связи!** ```r ?predict.glm ``` <br/> ]] --- ## Предсказания модели при помощи операций с матрицами ```r # Модельная матрица и коэффициенты X <- model.matrix(~ Treatment + DiversityD_1 + Flowers + Hours, data = NewData) betas <- coef(M_nb) # Предсказанные значения и стандартные ошибки... # ...в масштабе функции связи (логарифм) NewData$fit_eta <- X %*% betas NewData$SE_eta <- sqrt(diag(X %*% vcov(M_nb) %*% t(X))) # ...в масштабе отклика (применяем функцию, обратную функции связи) NewData$fit_mu <- exp(NewData$fit_eta) NewData$lwr <- exp(NewData$fit_eta - 2 * NewData$SE_eta) NewData$upr <- exp(NewData$fit_eta + 2 * NewData$SE_eta) head(NewData, 2) ``` ``` # A tibble: 2 × 9 # Groups: Treatment [1] Treatment Flowers DiversityD_1 Hours fit_eta[,1] SE_eta fit_mu[,1] lwr[,1] upr[,1] <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 Control 11 1.86 0.75 0.538 0.357 1.71 0.839 3.49 2 Control 11.7 1.86 0.75 0.560 0.351 1.75 0.867 3.53 ``` --- ## График предсказаний в масштабе функции связи ```r ggplot(NewData, aes(x = Flowers, y = fit_eta, fill = Treatment)) + geom_ribbon(aes(ymin = fit_eta - 2 * SE_eta, ymax = fit_eta + 2 * SE_eta), alpha = 0.5) + geom_line(aes(colour = Treatment)) + geom_hline(yintercept = 0) ``` <!-- --> В масштабе функции связи мы моделируем линейную зависимость логарифмов мат. ожидания отклика от предикторов. --- ## График предсказаний в масштабе отклика ```r ggplot(NewData, aes(x = Flowers, y = fit_mu, fill = Treatment)) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.3) + geom_line(aes(colour = Treatment)) + geom_hline(yintercept = 0) ``` <!-- --> GLM с отрицательным биномиальным распределением отклика моделирует его нелинейную связь предикторами за счет функции связи `\(log()\)`. --- ## GLM с отрицательным биномиальным распределением отклика GLM с отрицательным биномиальным распределением отклика до какой-то степени может учесть гетерогенность дисперсии ( `\(E(y_i) = \mu_i\)`, `\(var(y_i) = \mu_i + \frac{\mu_i^2}{k}\)`). На графике видно, что стандартные ошибки возрастают с увеличением предсказанного значения даже сильнее, чем это было у Пуассоновской модели. Этого оказалось вполне достаточно для моделирования данных (сверхдисперсии здесь нет). <!-- --> --- ## Выводы Число визитов опылителей на цветки мускари значимо зависит от разнообразия флоры на данном участке (тест отношения правдоподобий, `\(p = 0.02\)`). При этом, чем больше цветов самого мускари, тем больше прилетает опылителей (тест отношения правдоподобий, `\(p = 0.01\)`). Влияние присутствия вида-вселенца или его цветов не было выявлено. <!-- --> --- ## Take-home messages - Важно формулировать модель с учетом распределения зависимой переменной. При моделировании счетных данных используются: + распределение Пуассона, + отрицательное биномиальное распределение. -- - В моделях для счетных данных не должно быть избыточности дисперсии. Она может возникать по многим причинам, поэтому нет единого рецепта борьбы с ней: - В квази-пуассоновских GLM используются поправки для стандартных ошибок оценок коэффициентов модели. - В моделях, основанных на отрицательном биномиальном распределении, специальный параметр этого распределения "описывает" сверхдисперсию. --- ## Что почитать + Zuur, A.F. and Ieno, E.N., 2016. A protocol for conducting and presenting results of regression-type analyses. Methods in Ecology and Evolution, 7(6), pp.636-645. + Кабаков Р.И. R в действии. Анализ и визуализация данных на языке R. М.: ДМК Пресс, 2014 + Zuur, A., Ieno, E.N. and Smith, G.M., 2007. Analyzing ecological data. Springer Science & Business Media.