Вы узнаете

  • Об обобщенных смешанных линейных моделях (GLMM) и о функциях R, которые могут их рассчитать

Вы сможете

  • Построить обобщенную смешанную модель для бинарных данных.
  • Применить для построения модели функции из нескольких пакетов, реализованных в R.

Вспомним основные идеи работы с бинарными переменными

Вопросы

  • Какое распределение используют при работе с бинарными данными?
  • Сколько параметров в функции плотности вероятности этого распределения?
  • В каком соотношении находятся матожидание и дисперсия этого распределения?

Биномиальное распределение

\(f(y; N, \pi) = \frac{N!}{y! \times (N-y)!} \times \pi^y \times (1 - \pi)^{N-y}\)

Два параметра (\(N\), \(\pi\))

Среднее:    \(E(Y) = N \times \pi\)
Дисперсия: \(var(Y) = N \times \pi \times (1-\pi)\)
Параметр \(N\) определяет количество объектов в испытании
Парметр \(\pi\) - вероятность события (\(y = 1\))

Пределы варьирования

\(0 \le Y \le +\infty\),   \(Y\) целочисленные

Вопросы

  • Что такое шансы?

  • Что такое логиты?

  • Какую связывающую функцию обычно используются при работе с бинарными перменными отклика?

Шансы и логиты

Дискретный отклик: 1 или 0


Вероятност события: \(\pi = \frac{N_i}{N_{total}}\)


Шансы (odds): \(odds=\frac{\pi}{1-\pi}\)


Логиты (logit): \(ln(odds)=\ln(\frac{\pi}{1-\pi})\)

Связывающая функция для бинарных перменных отклика

Каноническая связывающая функция - логит-функция: \(\eta(\pi)=\ln(\frac{\pi}{1-\pi})\)

family = binomial(link = "logit")

Помимо логит-функции можно применить еще несколько:

Complementary Log-Log связывающая функция : \(\eta(\pi)=\ln(-\ln(1-\pi))\)
family = binomial(link = "cloglog")

Пробит - связывающая фунция: \(\eta(\pi)=\Phi^{-1}(\pi)\)
family = binomial(link = "probit")

Что где находится на этом графике?

Построение модели для бинарной переменной отклика

Морские желуди: Кого съедят бореотрофоны?

Данные взяты из работы
Yakovis Y., Artemieva A. "Bored to Death: Community-Wide Effect of Predation on a Foundation Species in a Low-Disturbance Arctic Subtidal System" PLOS, 2015. DOI: 10.1371/journal.pone.0132973

Вопрос: от каких факторов зависит будет ли атакован балянус хищником?

Мы будем оценивать связь вероятности гибели балянуса от нападения Boreotrophon clathratus.

Дизайн сбора материала

Читаем данные

bal <- read.table("data/Yakovis2.csv", header = TRUE, sep = ";")
#Some housekeeping
bal$Site <- factor(bal$Site)
bal$Sample <- factor(bal$Sample)
bal$Substrate_ID <- factor(bal$Substrate_ID)

Переменные

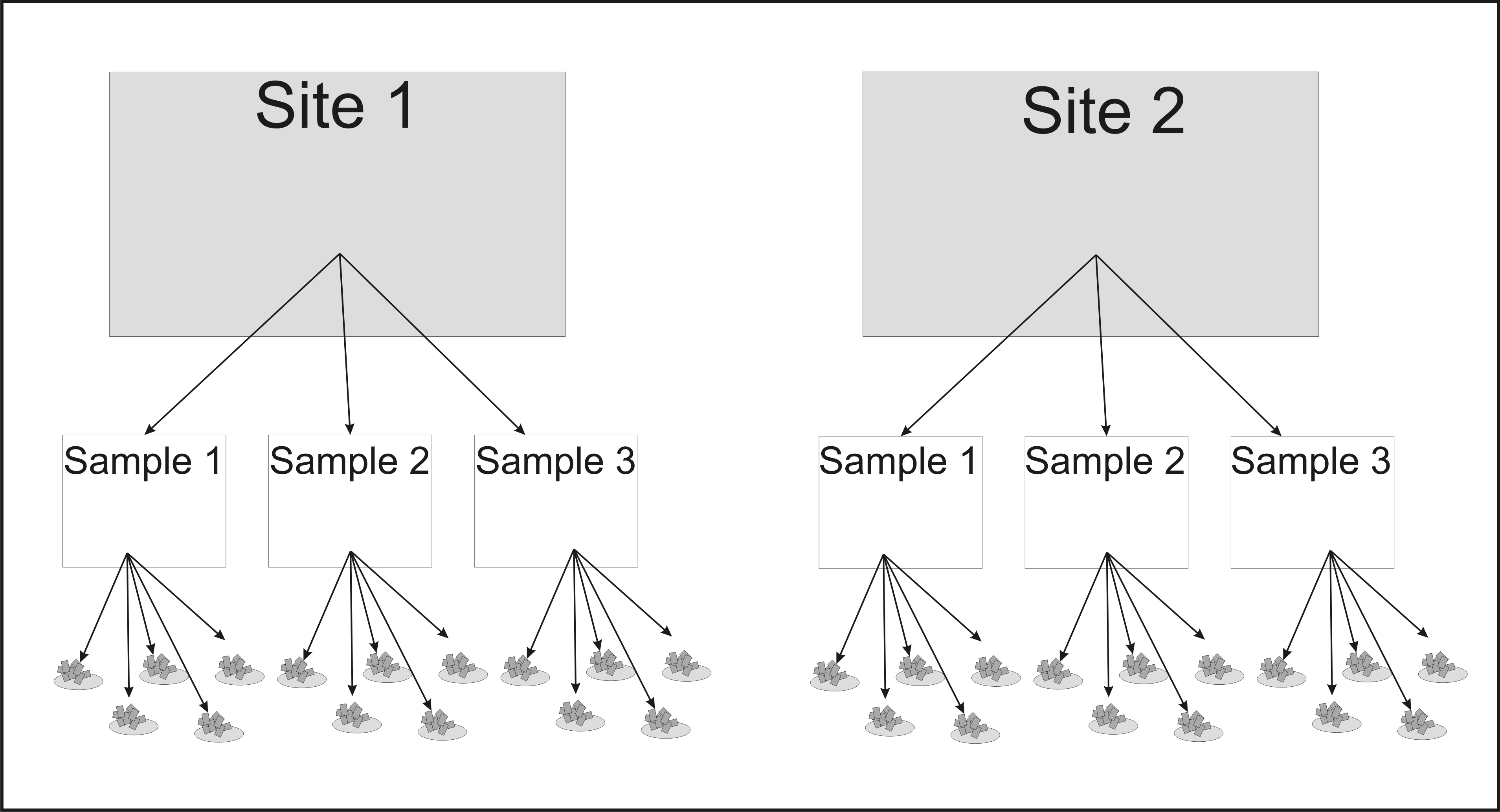
Site -точка сбора материала
Sample - квдарат 1х1 м, на котором производился сбор друз
BorN - количество Boreotrophon clathratus на квадрате
Substrate_ID - Номер друзы
ALength - Диаметр апертуры
Age - Возраст балянуса
Position - Расположение балянуса (первичный субстрат/вторичный субстрат)
Status - живой/мертвый

Drill - Зависимая переменная (0 - нет следов сверления; 1 - есть следы сверления)

Для ответа на поставленный вопрос целесообразно работать с мертвыми особями

Задание

Вычислите какая доля живых и мертвых особей несет следы сверления

Решение

bal1 <- bal[bal$Status == "live_barnacle", ]
mean(bal1$Drill ==1) 
## [1] 0.0128
bal2 <-  bal[bal$Status == "empty_test", ]
mean(bal2$Drill == 1) 
## [1] 0.0816

Задание

Напишите код, который задаст формулу для фиксированной части модели

Решение

Fix_effect <- formula(Drill ~ BorN + ALength + Age + Position + Site)

Задание

Напишите код, который задаст формулу для случайной части модели

Решение

Rand_effect <- formula(~1|Sample/Substrate_ID)

Согласно дизайну сбора материала, необходимо построить обобщенную смешанную линейную модель (GLMM)

Функция максимального правдоподобия для GLMM

\[Lik(\beta, D) = \Pi_i\int f(Y_i|b_i)\times f(b_i)db_i\]

Вычисление максимума функции правдоподобия для GLMM может производиться только в численном виде (аналитическое решение невозможно). Поэтому все алгоритмы очень затратны по времени.

Инструменты R, позволяющие подобрать GLMM

Пакет Функция Особенности работы функции
MASS glmPQL() Использует penalised quasi-likelihood (PQL) алгоритм, следовательно не выдает AIC. Выбор оптмальной модели может производиться только на основе оценок статистической значимсоти параметров (критерий Вальда). Работает быстро.
glmmML glmmML() Выдает значение AIC. Может использовать только один уровень группирующих факторов. Работает быстро.
lme4 glmer() Выдает значение AIC. Работает медленно. При сложных моделях часто не сходится.
glmmADMB glmmadmb() Выдает значение AIC. Работает ОЧЕНЬ медленно (Для сложных моделей и бльших объемов данных до нескольких часов).

Важно!Во всех случаях надо с осторожостью принимать решения при уровнях значимости близкх к 5%!
Альтернативный подход к построению сложных моделей - использование методов Байесовской статистики

Подбираем модель с помощью функции glmmPQL

library(MASS)

M1_PQL <- glmmPQL(Fix_effect, random = ~1|Sample/Substrate_ID, 
                  data = bal2, 
                  family = "binomial")

Результаты

summary(M1_PQL)
## Linear mixed-effects model fit by maximum likelihood
##  Data: bal2 
##   AIC BIC logLik
##    NA  NA     NA
## 
## Random effects:
##  Formula: ~1 | Sample
##         (Intercept)
## StdDev:       0.358
## 
##  Formula: ~1 | Substrate_ID %in% Sample
##         (Intercept) Residual
## StdDev:        1.62    0.704
## 
## Variance function:
##  Structure: fixed weights
##  Formula: ~invwt 
## Fixed effects: Drill ~ BorN + ALength + Age + Position + Site 
##                   Value Std.Error   DF t-value p-value
## (Intercept)       -4.12     0.445 1908   -9.25  0.0000
## BorN               0.07     0.053    6    1.35  0.2243
## ALength            0.15     0.046 1908    3.24  0.0012
## Age               -0.10     0.077 1908   -1.29  0.1969
## Positionsecondary  1.26     0.172 1908    7.34  0.0000
## Site2             -0.30     0.612    6   -0.49  0.6437
##  Correlation: 
##                   (Intr) BorN   ALngth Age    Pstnsc
## BorN              -0.776                            
## ALength           -0.232 -0.035                     
## Age                0.079  0.043 -0.907              
## Positionsecondary -0.314  0.047  0.025  0.169       
## Site2             -0.480  0.390 -0.021  0.042  0.069
## 
## Standardized Within-Group Residuals:
##    Min     Q1    Med     Q3    Max 
## -4.244 -0.366 -0.205 -0.116 13.809 
## 
## Number of Observations: 2120
## Number of Groups: 
##                   Sample Substrate_ID %in% Sample 
##                        9                      209

Подбираем модель с помощью функции glmmML()

library(glmmML)
M1_ML <- glmmML(Fix_effect, cluster = Substrate_ID, data = bal2)
M2_ML <- glmmML(Fix_effect, cluster = Sample, data = bal2)
# Коэффициенты
C_glmmML_1 <- round(as.numeric(coefficients(M1_ML)), 3)
C_glmmML_2 <- round(as.numeric(coefficients(M2_ML)), 3)

Результаты первой модели

glmmML::summary.glmmML(M1_ML)
## 
## Call:  glmmML(formula = Fix_effect, data = bal2, cluster = Substrate_ID) 
## 
## 
##                      coef se(coef)       z    Pr(>|z|)
## (Intercept)       -4.3674   0.4100 -10.653 0.000000000
## BorN               0.0869   0.0405   2.149 0.032000000
## ALength            0.1316   0.0609   2.162 0.031000000
## Age               -0.0677   0.1036  -0.653 0.510000000
## Positionsecondary  1.2967   0.2289   5.664 0.000000015
## Site2             -0.2901   0.5432  -0.534 0.590000000
## 
## Scale parameter in mixing distribution:  1.42 gaussian 
## Std. Error:                              0.164 
## 
##         LR p-value for H_0: sigma = 0:  4.77e-23 
## 
## Residual deviance: 1020 on 2113 degrees of freedom   AIC: 1030

Результаты второй модели

glmmML::summary.glmmML(M2_ML)
## 
## Call:  glmmML(formula = Fix_effect, data = bal2, cluster = Sample) 
## 
## 
##                      coef se(coef)      z Pr(>|z|)
## (Intercept)       -4.1523   0.4256 -9.757  0.0e+00
## BorN               0.1173   0.0491  2.388  1.7e-02
## ALength            0.0652   0.0515  1.266  2.1e-01
## Age                0.0360   0.0859  0.419  6.8e-01
## Positionsecondary  1.2242   0.1838  6.661  2.7e-11
## Site2              0.2051   0.5305  0.387  7.0e-01
## 
## Scale parameter in mixing distribution:  0.458 gaussian 
## Std. Error:                              0.137 
## 
##         LR p-value for H_0: sigma = 0:  0.00000327 
## 
## Residual deviance: 1090 on 2113 degrees of freedom   AIC: 1110

Подбираем модель с помощью функции glmer()

library(lme4)
M1_glmer <- glmer(Drill ~ BorN + ALength + Age + Position + Site +
                    (1|Sample/Substrate_ID), data = bal2, 
                  family = "binomial") 

C_glmer <- round(lme4::fixef(M1_glmer), 3)

Результаты

summary(M1_glmer)
## Generalized linear mixed model fit by maximum likelihood (Laplace
##   Approximation) [glmerMod]
##  Family: binomial  ( logit )
## Formula: 
## Drill ~ BorN + ALength + Age + Position + Site + (1 | Sample/Substrate_ID)
##    Data: bal2
## 
##      AIC      BIC   logLik deviance df.resid 
##     1033     1078     -508     1017     2112 
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -2.399 -0.262 -0.163 -0.101  9.177 
## 
## Random effects:
##  Groups              Name        Variance Std.Dev.
##  Substrate_ID:Sample (Intercept) 1.8578   1.363   
##  Sample              (Intercept) 0.0634   0.252   
## Number of obs: 2120, groups:  Substrate_ID:Sample, 209; Sample, 9
## 
## Fixed effects:
##                   Estimate Std. Error z value    Pr(>|z|)    
## (Intercept)        -4.4040     0.4510   -9.76     < 2e-16 ***
## BorN                0.0941     0.0479    1.96       0.050 *  
## ALength             0.1270     0.0614    2.07       0.039 *  
## Age                -0.0605     0.1042   -0.58       0.561    
## Positionsecondary   1.3065     0.2290    5.71 0.000000012 ***
## Site2              -0.2308     0.5862   -0.39       0.694    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) BorN   ALngth Age    Pstnsc
## BorN        -0.698                            
## ALength     -0.295 -0.077                     
## Age          0.103  0.086 -0.912              
## Postnscndry -0.433  0.082  0.032  0.148       
## Site2       -0.417  0.396 -0.050  0.074  0.090
## convergence code: 0
## Model failed to converge with max|grad| = 0.00113631 (tol = 0.001, component 1)

Сравним коэффициенты, подобранные разными функциями

          Parameter glmmPQL glmmML_1  glmmML_2  glmer
1       (Intercept)  -4.119   -4.367   -4.152  -4.404
2              BorN   0.072    0.087*   0.117*  0.094*
3           ALength   0.148*   0.132*   0.065   0.127*
4               Age  -0.100   -0.068    0.036  -0.061
5 Positionsecondary   1.261*   1.297*   1.224*  1.306*
6             Site2  -0.298   -0.290    0.205  -0.231

Выбор на совести исследователя!

Выбор оптимальной модели

drop1(M1_glmer)
## Single term deletions
## 
## Model:
## Drill ~ BorN + ALength + Age + Position + Site + (1 | Sample/Substrate_ID)
##          Df  AIC
## <none>      1033
## BorN      1 1035
## ALength   1 1035
## Age       1 1031
## Position  1 1064
## Site      1 1031

Выбор оптимальной модели

M2_glmer <- update(M1_glmer, .~.- Site)
anova(M1_glmer, M2_glmer)
## Data: bal2
## Models:
## M2_glmer: Drill ~ BorN + ALength + Age + Position + (1 | Sample/Substrate_ID)
## M1_glmer: Drill ~ BorN + ALength + Age + Position + Site + (1 | Sample/Substrate_ID)
##          Df  AIC  BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## M2_glmer  7 1031 1071   -509     1017                        
## M1_glmer  8 1033 1078   -508     1017  0.15      1       0.69

Выбор оптимальной модели

drop1(M2_glmer)
## Single term deletions
## 
## Model:
## Drill ~ BorN + ALength + Age + Position + (1 | Sample/Substrate_ID)
##          Df  AIC
## <none>      1031
## BorN      1 1034
## ALength   1 1033
## Age       1 1029
## Position  1 1063

Выбор оптимальной модели

M3_glmer <- update(M2_glmer, .~.-Age)
anova(M2_glmer, M3_glmer)
## Data: bal2
## Models:
## M3_glmer: Drill ~ BorN + ALength + Position + (1 | Sample/Substrate_ID)
## M2_glmer: Drill ~ BorN + ALength + Age + Position + (1 | Sample/Substrate_ID)
##          Df  AIC  BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## M3_glmer  6 1029 1063   -509     1017                        
## M2_glmer  7 1031 1071   -509     1017  0.31      1       0.58

Выбор оптимальной модели

drop1(M3_glmer)
## Single term deletions
## 
## Model:
## Drill ~ BorN + ALength + Position + (1 | Sample/Substrate_ID)
##          Df  AIC
## <none>      1029
## BorN      1 1032
## ALength   1 1042
## Position  1 1064

Результаты

summary(M3_glmer)
## Generalized linear mixed model fit by maximum likelihood (Laplace
##   Approximation) [glmerMod]
##  Family: binomial  ( logit )
## Formula: 
## Drill ~ BorN + ALength + Position + (1 | Sample/Substrate_ID)
##    Data: bal2
## 
##      AIC      BIC   logLik deviance df.resid 
##     1029     1063     -509     1017     2114 
## 
## Scaled residuals: 
##    Min     1Q Median     3Q    Max 
## -2.371 -0.262 -0.163 -0.103  9.193 
## 
## Random effects:
##  Groups              Name        Variance Std.Dev.
##  Substrate_ID:Sample (Intercept) 1.8092   1.345   
##  Sample              (Intercept) 0.0773   0.278   
## Number of obs: 2120, groups:  Substrate_ID:Sample, 209; Sample, 9
## 
## Fixed effects:
##                   Estimate Std. Error z value     Pr(>|z|)    
## (Intercept)        -4.4498     0.4108  -10.83      < 2e-16 ***
## BorN                0.1035     0.0450    2.30      0.02154 *  
## ALength             0.0948     0.0252    3.76      0.00017 ***
## Positionsecondary   1.3335     0.2256    5.91 0.0000000034 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) BorN   ALngth
## BorN        -0.663              
## ALength     -0.517 -0.015       
## Postnscndry -0.462  0.040  0.411

Проверка валидности модели

plot(M3_glmer)

Проверка валидности модели

Визуализация предсказаний модели

Summary

  • Построение обобщенных смешанных моделей (GLMM) для бинарных перменных отклика аналогично построению моделей для GLM и LMM.
  • Идеального алгоритма для построения GLMM пока нет.
  • Существующие ныне алгоритмы пригодны только для простых моделей.

Что почитать

  • Zuur, A.F. et al. 2009. Mixed effects models and extensions in ecology with R. - Statistics for biology and health. Springer, New York, NY.