Кластерный анализ

# Кластерный анализ
## Анализ и визуализация многомерных данных с использованием R
### Марина Варфоломеева
### Вадим Хайтов

---

## Кластерный анализ

- Методы построения деревьев
- Методы кластеризации на основании расстояний
- Примеры для демонстрации и для заданий
- Кластерный анализ в R
- Качество кластеризации:
    - кофенетическая корреляция
    - ширина силуэта
    - поддержка ветвей
- Сопоставление деревьев: танглграммы

### Вы сможете

- Выбирать подходящий метод агрегации (алгоритм кластеризации)
- Строить дендрограммы
- Оценивать качество кластеризации (Кофенетическая корреляция, ширина силуэта, поддержка ветвей)
- Сопоставлять дендрограммы, полученные разными способами, при помощи танглграмм

---

# Кластерный анализ

---

## Какие бывают методы построения деревьев?

### Методы кластеризации на основании расстояний (о них сегодня)
  - Метод ближайшего соседа
  - Метод отдаленного соседа
  - Метод среднегруппового расстояния
  - Метод Варда
  - и т.д. и т.п.

### Методы кластеризации на основании признаков
  - Метод максимальной бережливости
  - Метод максимального правдоподобия

### И это еще далеко не все

---

# Пример: Волки

---

## Пример: Волки

Морфометрия черепов у волков в Скалистых горах и в Арктике (Jolicoeur, 1959)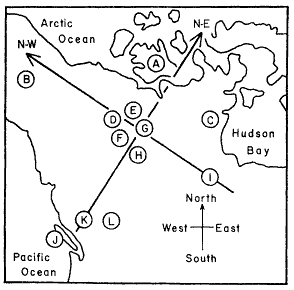

![Map from Jolicoeur 1959](images/Wolves_map_Jolicoeur_1959.png)

Данные взяты из работы Morrison (1990):

- A --- волки из Арктики (10 самцов, 6 самок)
- L --- волки из Скалистых гор (6 самцов, 3 самки)

```r
library(candisc)
data("Wolves")
```

---

## Знакомимся с данными

```r
dim(Wolves)
```

```
## [1] 25 12
```

```r
colnames(Wolves)
```

```
##  [1] "group"    "location" "sex"      "x1"       "x2"       "x3"      
##  [7] "x4"       "x5"       "x6"       "x7"       "x8"       "x9"
```

```r
head(rownames(Wolves))
```

```
## [1] "rmm1" "rmm2" "rmm3" "rmm4" "rmm5" "rmm6"
```

```r
any(is.na(Wolves))
```

```
## [1] FALSE
```

```r
table(Wolves$group)
```

```
## 
## ar:f ar:m rm:f rm:m 
##    6   10    3    6
```

---

## Задание

- Постройте ординацию nMDS данных
- Оцените качество ординации
- Обоснуйте выбор коэффициента
- Раскрасьте точки на ординации волков в зависимости от географического происхождения (`group`)

---

## Решение

```r
library(vegan)
library(ggplot2); theme_set(theme_bw(base_size = 16))
s_w <- scale(Wolves[, 4:ncol(Wolves)]) ## стандартизируем
ord_w <- metaMDS(comm = s_w, distance = "euclidean", autotransform = FALSE)
dfr_w <- data.frame(ord_w$points, Group = Wolves$group)
gg_w <- ggplot(dfr_w, aes(x = MDS1, y = MDS2)) + geom_point(aes(colour = Group))
```

```
## Run 0 stress 0.101 
## Run 1 stress 0.128 
## Run 2 stress 0.128 
## Run 3 stress 0.126 
## Run 4 stress 0.136 
## Run 5 stress 0.101 
## ... New best solution
## ... Procrustes: rmse 0.00000401  max resid 0.0000114 
## ... Similar to previous best
## Run 6 stress 0.127 
## Run 7 stress 0.156 
## Run 8 stress 0.101 
## ... Procrustes: rmse 0.00000411  max resid 0.0000136 
## ... Similar to previous best
## Run 9 stress 0.137 
## Run 10 stress 0.101 
## ... Procrustes: rmse 0.00000633  max resid 0.0000208 
## ... Similar to previous best
## Run 11 stress 0.127 
## Run 12 stress 0.127 
## Run 13 stress 0.101 
## ... Procrustes: rmse 0.00000696  max resid 0.000023 
## ... Similar to previous best
## Run 14 stress 0.137 
## Run 15 stress 0.128 
## Run 16 stress 0.101 
## ... New best solution
## ... Procrustes: rmse 0.00000302  max resid 0.00000761 
## ... Similar to previous best
## Run 17 stress 0.101 
## ... Procrustes: rmse 0.00000467  max resid 0.0000131 
## ... Similar to previous best
## Run 18 stress 0.127 
## Run 19 stress 0.136 
## Run 20 stress 0.147 
## *** Solution reached
```
]

---

## Решение

---

# Методы кластеризации на основании расстояний

---

## Этапы кластеризации

.pull-left[
<div id="htmlwidget-f62c96e0ee521dc7a21c" style="width:432px;height:504px;" class="DiagrammeR html-widget"></div>
<script type="application/json" data-for="htmlwidget-f62c96e0ee521dc7a21c">{"x":{"diagram":"graph TD; \n           A(Набор признаков)-->B(Матрица расстояний или сходств); \n           B-->C(Группировка объектов);\n           C-->D(Отношения между кластерами); D-->E(Поправки); E-->A;\n  "},"evals":[],"jsHooks":[]}</script>
]

Результат кластеризации зависит от

- выбора признаков
- коэффициента сходства-различия
- от алгоритма кластеризации

]

---

## Методы кластеризации

---

## Метод ближайшего соседа

### = nearest neighbour = single linkage

- к кластеру присоединяется ближайший к нему кластер/объект
- кластеры объединяются в один на расстоянии, которое равно расстоянию между ближайшими объектами этих кластеров
]
]

<img src="05_cluster_analysis_files/figure-html/unnamed-chunk-7-1.png" style="display: block; margin: auto;" />
]

### Особенности

- Может быть сложно интерпретировать, если нужны группы
  - объекты на дендрограмме часто не образуют четко разделенных групп
  - часто получаются цепочки кластеров (объекты присоединяются как бы по-одному)
- Хорош для выявления градиентов

---

## Как работает метод ближайшего соседа

---

## Как работает метод ближайшего соседа

---

## Метод отдаленного соседа

### = furthest neighbour = complete linkage

- к кластеру присоединяется отдаленный кластер/объект
- кластеры объединяются в один на расстоянии, которое равно расстоянию между самыми отдаленными объектами этих кластеров (следствие - чем более крупная группа, тем сложнее к ней присоединиться)
]]

]

### Особенности

- На дендрограмме образуется много отдельных некрупных групп
- Хорош для поиска дискретных групп в данных

---

## Как работает метод отдаленного соседа

---

## Как работает метод отдаленного соседа

---

## Метод невзвешенного попарного среднего

### = UPGMA = Unweighted Pair Group Method with Arithmetic mean

- кластеры объединяются в один на расстоянии, которое равно среднему значению всех возможных расстояний между объектами из разных кластеров.
]]
.pull-right-33[

]

### Особенности

- UPGMA и WUPGMС иногда могут приводить к инверсиям на дендрограммах
.pull-left-66[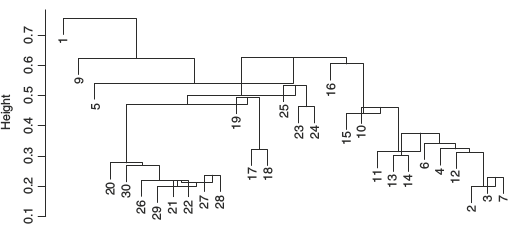
![Инверсии на дендрограммах](images/clust-revert.png)
]
.pull-right-33[
.pull-down[
из Borcard et al., 2011
]]

---

## Как работает метод среднегруппового расстояния

---

## Метод Варда

### = Ward's Minimum Variance Clustering

- объекты объединяются в кластеры так, чтобы внутригрупповая дисперсия расстояний была минимальной
]]

<img src="05_cluster_analysis_files/figure-html/unnamed-chunk-12-1.png" style="display: block; margin: auto;" />
]

### Особенности

- метод годится и для неевклидовых расстояний несмотря на то, что внутригрупповая дисперсия расстояний рассчитывается так, как будто это евклидовы расстояния

---

## Как работает метод Варда

---

# Кластерный анализ в R

---

## Кластеризация

Давайте построим деревья при помощи нескольких алгоритмов кластеризации (по стандартизованным данным, с использованием Евклидова расстояния) и сравним их.

```r
# Матрица расстояний
d <- dist(x = s_w, method = "euclidean")
# Пакеты для визуализации кластеризации
library(ape)
library(dendextend)
```

---

## (1.0) Метод ближайшего соседа + `base`

```r
hc_single <- hclust(d, method = "single")
plot(hc_single)
```

---

## (1.1) Метод ближайшего соседа + `ape`

```r
ph_single <- as.phylo(hc_single)
plot(ph_single, type = "phylogram")
axisPhylo()
```

---

## (1.2) Метод ближайшего соседа + `dendextend`

```r
den_single <- as.dendrogram(hc_single)
plot(den_single)
```

---

## (2.1) Метод отдаленного соседа + `ape`

```r
hc_compl <- hclust(d, method = "complete")
ph_compl <- as.phylo(hc_compl)
plot(ph_compl, type = "phylogram")
axisPhylo()
```

---

## (2.2)Метод отдаленного соседа + `dendextend`

```r
den_compl <- as.dendrogram(hc_compl)
plot(den_compl)
```

---

## (3.1) Метод невзвешенного попарного среднего + `ape`

```r
hc_avg <- hclust(d, method = "average")
ph_avg <- as.phylo(hc_avg)
plot(ph_avg, type = "phylogram")
axisPhylo()
```

---

## (3.2) Метод невзвешенного попарного среднего + `dendextend`

```r
den_avg <- as.dendrogram(hc_avg)
plot(den_avg)
```

---

## (4.1) Метод Варда + `ape`

```r
hc_w2 <-hclust(d, method = "ward.D2")
ph_w2 <- as.phylo(hc_w2)
plot(ph_w2, type = "phylogram")
axisPhylo()
```

---

## (4.2) Метод Варда + `dendextend`

```r
den_w2 <- as.dendrogram(hc_w2)
plot(den_w2)
```

---

# Качество кластеризации

---

## Кофенетическая корреляция

__Кофенетическое расстояние__ - расстояние между объектами на дендрограмме

.content-box-purple[
__Кофенетическая корреляция__ - мера качества отображения многомерных данных на дендрограмме. Кофенетическую корреляцию можно рассчитать как Пирсоновскую корреляцию (обычную) между матрицами исходных и кофенетических расстояний между всеми парами объектов
]

<br/>

Метод агрегации, который дает наибольшую кофенетическую корреляцию, дает кластеры, лучше всего отражающие исходные данные

Можно рассчитать при помощи функции из пакета `ape`

---

## Кофенетическая корреляция в R

```r
# Матрица кофенетических расстояний 
c_single <- cophenetic(ph_single)

# Кофенетическая корреляция = 
# = корреляция матриц кофенетич. и реальн. расстояний
cor(d, as.dist(c_single))
```

```
## [1] 0.565
```

---

## Задание:

Оцените при помощи кофенетической корреляции качество кластеризаций, полученных разными методами.

Какой метод дает лучший результат?

---

## Решение:

```r
c_single <- cophenetic(ph_single)
cor(d, as.dist(c_single))
```

```
## [1] 0.565
```

```r
c_compl <- cophenetic(ph_compl)
cor(d, as.dist(c_compl))
```

```
## [1] 0.706
```

```r
c_avg <- cophenetic(ph_avg)
cor(d, as.dist(c_avg))
```

```
## [1] 0.745
```

```r
c_w2 <- cophenetic(ph_w2)
cor(d, as.dist(c_w2))
```

```
## [1] 0.726
```

---

## Что можно делать дальше с дендрограммой

- Можно выбрать число кластеров: 
    + либо субъективно, на любом выбранном уровне (главное, чтобы кластеры были осмысленными и интерпретируемыми);
    + либо исходя из распределения расстояний ветвления.
- Можно оценить стабильность кластеризации при помощи бутстрепа.

---

## Ширина силуэта

.content-box-purple[
Ширина силуэта `$s_i$` --- мера степени принадлежности объекта `$i$` к кластеру 
]

`$$s_i = \frac {\color{purple}{\bar{d}_{i~to~nearest~cluster}} - \color{green}{\bar{d}_{i~within}}} {max\{\color{purple}{\bar{d}_{i~to~nearest~cluster}}, \color{green}{\bar{d}_{i~within}}\}}$$`

`$s_i$` --- сравнивает между собой средние расстояния от данного объекта:
- `$\color{green} {\bar{d}_{i~within}}$` --- до других объектов из того же кластера
- `$\color{purple} {\bar{d}_{i~to~nearest~cluster}}$` --- до ближайшего кластера

`$-1 \le s_i \le 1$` --- чем больше `$s_i$`, тем "лучше" объект принадлежит кластеру.

- Средняя ширина силуэта для всех объектов из кластера --- оценивает, насколько "тесно" сгруппированы объекты.
- Средняя ширина силуэта по всем данным --- оценивает общее качество классификации.
- Чем больше к 1, тем лучше. Если меньше 0.25, то можно сказать, что нет структуры.

---

## Как рассчитывается ширина силуэта

Оценим ширину силуэта для 3 кластеров

```r
library(cluster)
complete3 <- cutree(tree = hc_avg, k = 3)
plot(silhouette(x = complete3, dist = d), cex.names = 0.6)
```

---

## Бутстреп поддержка ветвей

"An approximately unbiased test of phylogenetic tree selection" (Shimodaria, 2002)

Этот тест использует специальный вариант бутстрепа --- multiscale bootstrap. Мы не просто многократно берем бутстреп-выборки и оцениваем для них вероятность получения топологий (BP p-value), эти выборки еще и будут с разным числом объектов. По изменению BP при разных объемах выборки можно вычислить AU (approximately unbiased p-value).

```r
library(pvclust)
# итераций должно быть 1000 и больше, здесь мало для скорости
cl_boot <- pvclust(t(s_w), method.hclust = "average", nboot = 100, 
                   method.dist = "euclidean", parallel = TRUE, iseed = 42)
```

```
## Creating a temporary cluster...done:
## socket cluster with 7 nodes on host 'localhost'
## Multiscale bootstrap... Done.
```

Обратите внимание на число итераций: `nboot = 100` --- это очень мало. На самом деле нужно 10000 или больше.

---

## Дерево с величинами поддержки

AU --- approximately unbiased p-values (красный),
BP --- bootstrap p-values (зеленый)

```r
plot(cl_boot)
# pvrect(cl_boot) # достоверные ветвления
```

---

## Для диагностики качества оценок AU

График стандартных ошибок для AU p-value нужен, чтобы оценить точность оценки самих AU. Чем больше было бутстреп-итераций, тем точнее будет оценка AU.

```r
seplot(cl_boot)
# print(cl_boot) # все значения
```

---

# Сопоставление деревьев: Танглграммы

---

## Танглграмма

Два дерева (с непохожим ветвлением) выравнивают, вращая случайным образом ветви вокруг оснований. Итеративный алгоритм. Картина каждый раз разная.

```r
set.seed(395)
untang_w <- untangle_step_rotate_2side(den_compl, den_w2, print_times = F)

# танглграмма
tanglegram(untang_w[[1]], untang_w[[2]],
           highlight_distinct_edges = FALSE,
           common_subtrees_color_lines = F,
           main = "Tanglegram",
           main_left = "Left tree",
           main_right = "Right tree",
           columns_width = c(8, 1, 8),
           margin_top = 3.2, margin_bottom = 2.5,
           margin_inner = 4, margin_outer = 0.5,
           lwd = 1.2, edge.lwd = 1.2, 
           lab.cex = 1.5, cex_main = 2)
```

---

## Танглграмма

---

## Задание

Постройте танглграмму из дендрограмм, полученных методом ближайшего соседа и методом Варда.

---

# Деревья по генетическим данным

---

## И небольшая демонстрация - дерево по генетическим данным

```r
webpage <-"http://evolution.genetics.washington.edu/book/primates.dna"
primates.dna <- read.dna(webpage)
d_pri <- dist.dna(primates.dna)
hc_pri <- hclust(d_pri, method = "average")
ph_pri <- as.phylo(hc_pri)
plot(ph_pri)
axisPhylo()
```

---

## Take-home messages

- Результат кластеризации зависит не только от выбора коэффициента, но и от выбора алгоритма.
- Качество кластеризации можно оценить разными способами.
- Кластеризации, полученные разными методами, можно сравнить на танглграммах.

---

## Дополнительные ресурсы

- Borcard, D., Gillet, F., Legendre, P., 2011. Numerical ecology with R. Springer.
- Legendre, P., Legendre, L., 2012. Numerical ecology. Elsevier.
- Quinn, G.G.P., Keough, M.J., 2002. Experimental design and data analysis for biologists. Cambridge University Press.

---

## И еще ресурсы

Как работает UPGMA можно посмотреть здесь:

- http://www.southampton.ac.uk/~re1u06/teaching/upgma/

Как считать поддержку ветвей (пакет + статья):

- pvclust: An R package for hierarchical clustering with p-values [WWW Document], n.d. URL http://www.sigmath.es.osaka-u.ac.jp/shimo-lab/prog/pvclust/ (accessed 11.7.14).

Для анализа молекулярных данных:

- Paradis, E., 2011. Analysis of Phylogenetics and Evolution with R. Springer.

---

## Данные для самостоятельной работы

### Фораминиферы маршей Белого моря (Golikova et al. 2020)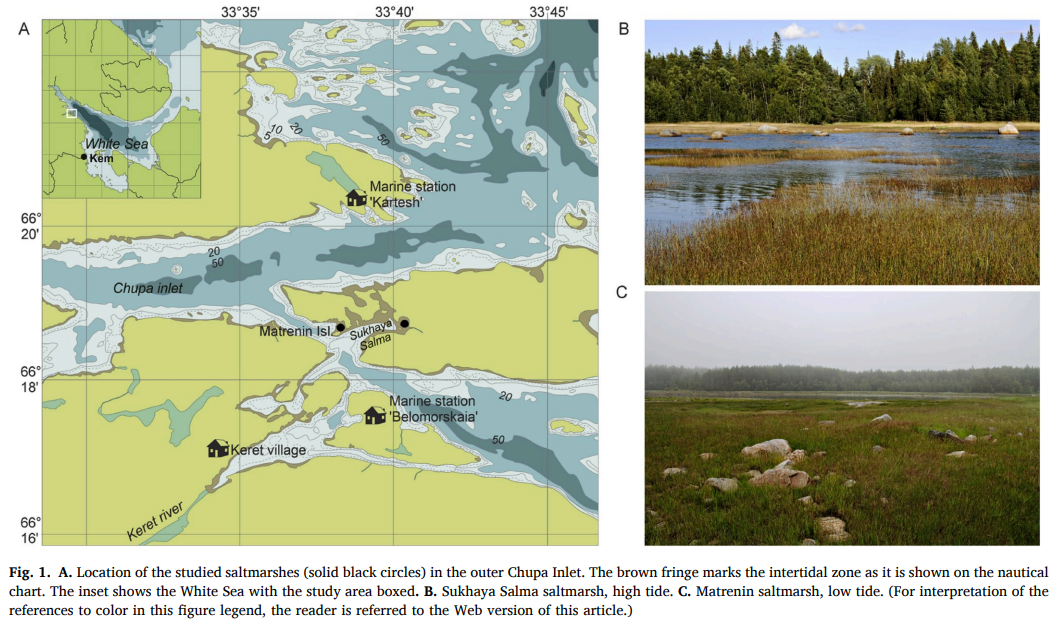

![map](images/Golikova_etal_2020_Fig1.png)
---

## Фораминиферы маршей Белого моря

![transect](images/Golikova_etal_2020_fig2.png)
---

## Фораминиферы маршей Белого моря

Plate 1.

1. _Balticammina pseudomacrescens_. 
2. _Ammotium salsum_. 
3. _Jadammina macrescens_. 
4. _Trochammina inflata_. 
5. _Ammobaculites balkwilli?_ 
6. _Miliammina fusca_. 
7. _Ovammina opaca_. 
8. _Elphidium albiumbilicatum_. 
9. _Elphidium williamsoni_.

Scale bar 500 μm.

]

---

## Задание

Проанализируйте данные об относительных обилиях фораминифер в пробах на Белом море.

- Выберите и обоснуйте трансформацию данных и расстояние.

- Постройте ординацию nMDS по относительным обилиям фораминифер:
  - цвет значков --- растение-доминант, 
  - форма значков --- точка сбора.

- Постройте дендрограмму проб по сходству отн. обилий фораминифер.
  - оцените при помощи кофенетической корреляции, какой метод аггрегации лучше,

- Опишите получившиеся кластеры при помощи различных параметров:
  - ширина силуэта
  - бутстреп-поддержка ветвлений

---

## Фораминиферы маршей Белого моря

![nMDS](images/Golikova_etal_2020_fig5.png)

---

## Фораминиферы маршей Белого моря

![dendrogram](images/Golikova_etal_2020_fig6.png)