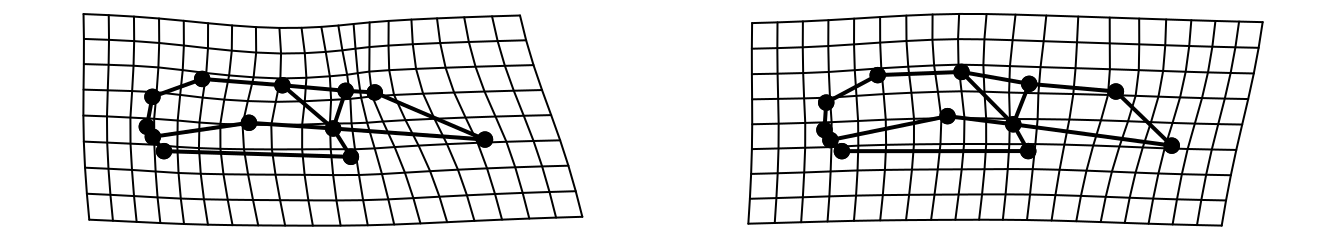Для анализа формы различных структур анализируются расстояния между метками, а не их координаты.
Признаки сильно интегрированных структур, например частей скелета, лучше анализировать совместно друг с другом. Один из вариантов анализа - анализ главных компонент.
Черепахи - единственные живые представители анапсид (череп не имеет височных окон). Морфология черепа важна для их систематики (Claude et al., 2004).
Данные - 24 разных измерения черепов черепах 122 ныне живущих пресноводных, морских и наземных видов и одного ископаемого.
Морфометрия черепах
turt <- read.table("data/turtles.txt", header = TRUE)
turt$Environment3 <- factor(turt$Environment3, levels = c(0, 1, 2, 9), labels = c("Freshwater", "Terrestrial", "Marine", "Fossil"))
colnames(turt)
## [1] "nspecies" "species_name" "Family" "SuperFamily" ## [5] "Order" "Environment" "Environment3" "D1" ## [9] "D2" "D3" "D4" "D5" ## [13] "D6" "D7" "D8" "D9" ## [17] "D10" "D11" "D12" "D13" ## [21] "D14" "D15" "D16" "D17" ## [25] "D18" "D19" "D20" "D21" ## [29] "D22" "D23" "D24"
boxplot(x = turt[8:31])
library(vegan)
## Loading required package: permute
## Loading required package: lattice
## This is vegan 2.5-7
turt_pca <- rda(turt[, 8:31], scale = TRUE)
eig <- eigenvals(turt_pca)[1:5] eig*100/sum(eig) # доля объясненной изменчивости
## PC1 PC2 PC3 PC4 PC5 ## 86.76 6.94 3.07 1.96 1.27
screeplot(turt_pca, bstick = TRUE)
biplot(turt_pca, display = "species", scaling = 2)
Как вы думаете, почему у всех переменных большие нагрузки по первой компоненте?
Что отражает первая компонента?
Нам достаточно центрировать строки, т.к. столбцы будут центрированы автоматически в процессе анализа главных компонент.
# Функция, которая может центрировать вектор
center <- function(x){
x - mean(x, na.rm = TRUE)
}
# применяем эту функцию к каждой строке
dbcent <- t(apply(turt[, 8:31], 1, center))
# получившийся датафрейм пришлось транспонировать,
# поскольку apply() результаты от каждой строки
# возвращает в виде столбцов
turt_db_pca <- rda(dbcent) eig_db <- eigenvals(turt_db_pca)[1:5] eig_db*100/sum(eig_db)
## PC1 PC2 PC3 PC4 PC5 ## 65.48 23.12 6.36 3.13 1.91
screeplot(turt_db_pca, bstick = TRUE)
biplot(turt_db_pca, display = "species", scaling = 2)
Интерпретируем как обычно: компонента отражает несколько признаков
op <- par(mfrow = c(1, 2), mar = c(4, 4, 0.5, 0.5), cex = 1.3)
biplot(turt_db_pca, display = "species", scaling = 2)
# цвета для графика факторных координат
colvec <- c("orange2", "limegreen", "steelblue", "red3")
# пустой график
plot(turt_db_pca, type = "n", scaling = 1)
# точки, раскрашенные по уровням фактора turt$Environment3
points(turt_db_pca, display = "sites", scaling = 1, pch = 21,
col = colvec[turt$Environment3], bg = colvec[turt$Environment3])
# легенда
legend("bottomright", legend = levels(turt$Environment3), bty = "n", pch = 21,
col = colvec, pt.bg = colvec)
par(op)
Plethodon jordani и P.teyahalee встречаются вместе и раздельно. В совместно обитающих популяциях меняется форма головы обоих видов. В разных группах популяций этот процесс параллельно приводит к одинаковым результатам. По-видимому, одной из причин параллельной эволюции может быть межвидовая конкуренция (Adams, 2004, 2010).
Plethodon jordani
Plethodon jordani - Jordan’s Salamander by John P Clare on Flickr
Plethodon cf. teyahalee
Plethodon cf. teyahalee by squamatologist on Flickr
Схема измерений
# install.packages("geomorph", dependencies = TRUE)
library(geomorph)
## Loading required package: RRPP
## Loading required package: rgl
## This build of rgl does not include OpenGL functions. Use ## rglwidget() to display results, e.g. via options(rgl.printRglwidget = TRUE).
## Loading required package: Matrix
data(plethodon) str(plethodon, vec.len = 2, give.attr = F)
## List of 5 ## $ land : num [1:12, 1:2, 1:40] 8.89 9.27 ... ## $ links : num [1:14, 1:2] 4 3 2 1 1 ... ## $ species: Factor w/ 2 levels "Jord","Teyah": 1 1 1 1 1 ... ## $ site : Factor w/ 2 levels "Allo","Symp": 2 2 2 2 2 ... ## $ outline: num [1:3631, 1:2] 0.399 0.4 ...
Все образцы разного размера и разной ориентации в пространстве. На этом графике — два образца для примера.
plotRefToTarget(plethodon$land[, , 1], plethodon$land[, ,10],
method = "points", mag = 1,
links = plethodon$links)
Слева - три образца, справа - все. Жирные точки - центроиды соответствующих меток
op <- par(mfrow = c(1, 2), mar = c(4, 4, 1, 1)) plotAllSpecimens(plethodon$land[, , 1:3], links=plethodon$links) plotAllSpecimens(plethodon$land,links=plethodon$links) par(op)
Прокрустово ложе
Тезей убивает разбойника Прокруста (источник https://mrpsmythopedia.wikispaces.com/Procrustes)
Generalized Procrustes Analysis (GPA)
Минимизируем сумму квадратов расстояний между одноименными метками, меняя масштаб, поворачивая и сдвигая координаты. Вот как это выглядит на данных про черепах:
Прокрустово преобразование
gpa <- gpagen(plethodon$land, print.progress = FALSE) plotAllSpecimens(gpa$coords,links=plethodon$links)
ref <- mshape(gpa$coords) plotRefToTarget(ref, ref, method = "TPS", links = plethodon$links)
Изменение формы можно представить графически несколькими способами
# матрица, в которой хранится разметка общего графика
m <- matrix(data = c(1, 2,
3, 3),
nrow = 2, ncol = 2, byrow = TRUE)
l <- layout(m, heights = c(1, 1), widths = c(1, 1))
# layout.show(l) # можно просмотреть разметку
# Графики
op <- par( mar = c(0, 0, 0, 0))
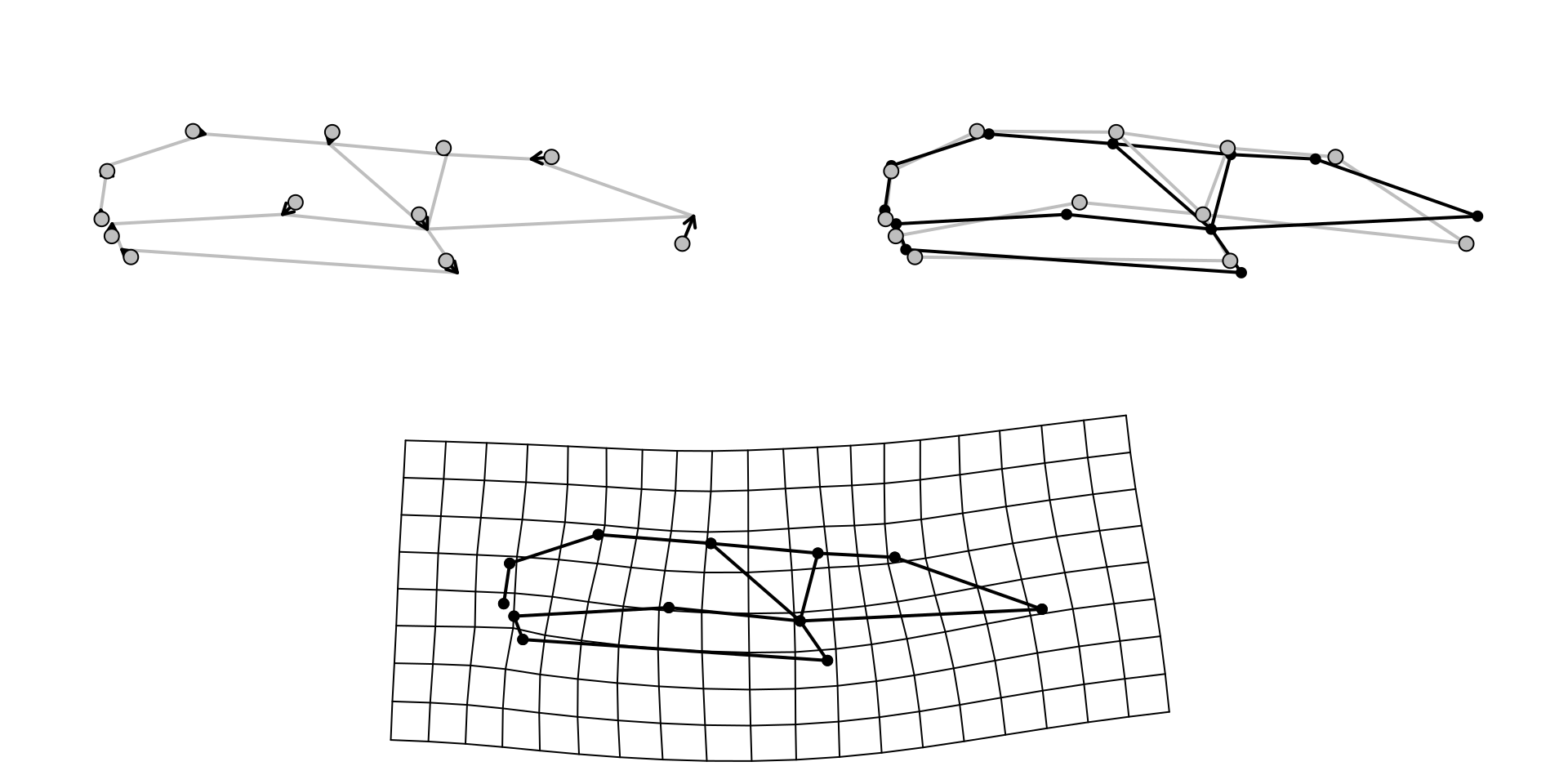
# 1) изменение конфигурации обозначено векторами
plotRefToTarget(ref, gpa$coords[, , 11],
method = "vector", mag = 1,
links = plethodon$links)
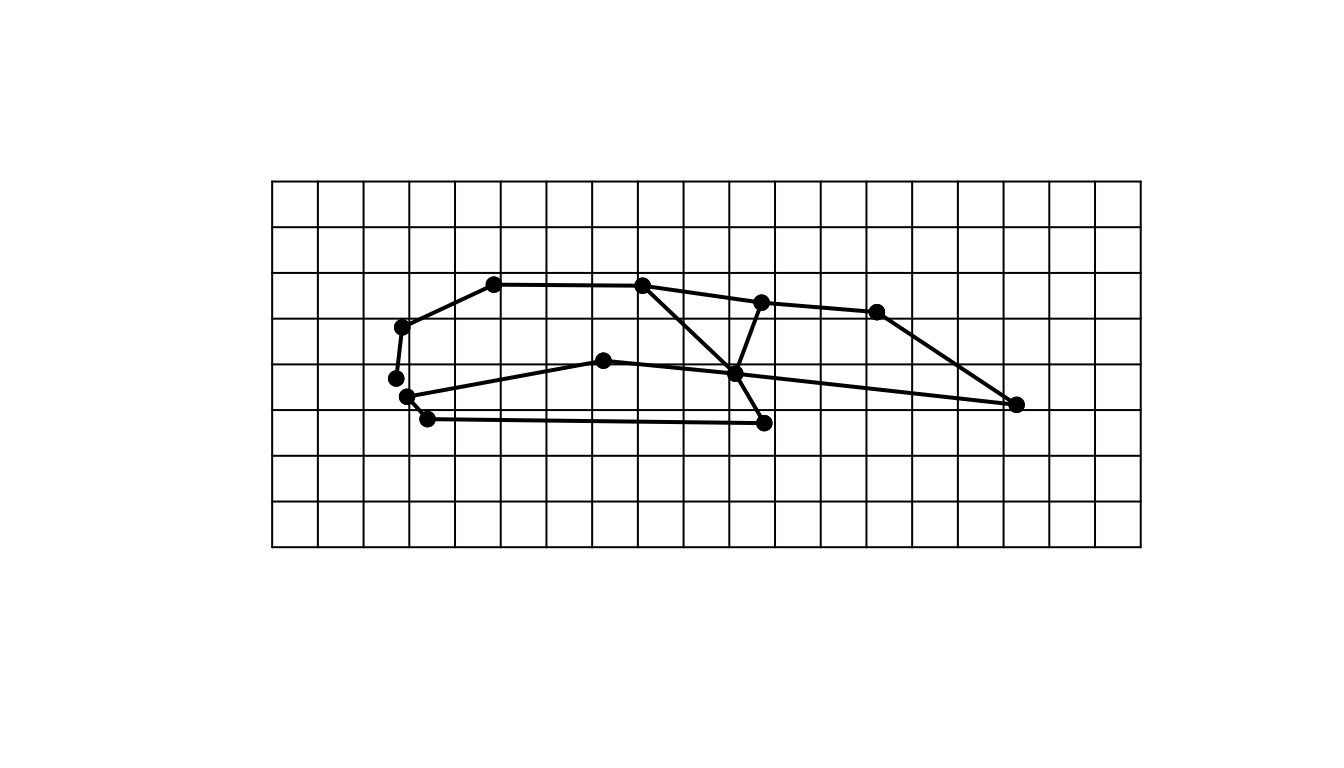
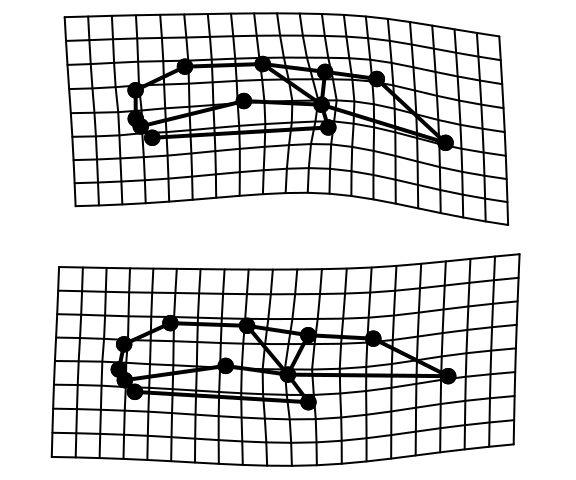
# 2) формы обозначены точками
plotRefToTarget(ref, gpa$coords[, , 11],
method = "points", mag = 1,
links = plethodon$links)
# 3) сплайн
plotRefToTarget(ref, gpa$coords[, , 11],
method = "TPS", mag = 1,
links = plethodon$links)
par(op)
Анализ главных компонент по координатам меток для выравненных образцов. Главные компоненты отражают изменения формы.
ord <- gm.prcomp(gpa$coords) plot(ord, main = "PCA")
op <- par(mar = c(4, 4, 1, 1))
gp <- as.factor(paste(plethodon$species, plethodon$site)) # группа должна быть фактором
# задаем соответствие цветов уровням фактора
colvec <- c("Jord Allo" = "yellow2",
"Jord Symp" = "orange",
"Teyah Allo" = "green4",
"Teyah Symp" = "green1")
# вектор цветов в порядке заданном фактором gp
colvec <- colvec[match(gp, names(colvec))]
# график
plot(ord, bg = colvec, pch = 21, col = "grey20")
# легенда
legend("topright", legend = levels(gp),
bty = "n", pch = 21,
col = "grey20",
pt.bg = levels(as.factor(colvec)))
par(op)
expl <- round(ord$d[1:5]/sum(ord$d) * 100, 1) # Доля изменчивости объясненной 1-5 компонентами head(ord$x[, 1:5]) # Факторные координаты по 1-5 компонентам
## Comp1 Comp2 Comp3 Comp4 Comp5 ## 1 -0.036993 0.0512 -0.001697 -0.00313 -0.01094 ## 2 -0.000749 0.0594 0.000137 -0.00277 -0.00812 ## 3 0.005600 0.0742 -0.005261 -0.00503 -0.00275 ## 4 -0.013481 0.0646 -0.045844 -0.00789 0.00982 ## 5 -0.033470 0.0686 0.013629 0.00736 0.02235 ## 6 -0.005214 0.0616 -0.029933 -0.00575 -0.02406
plot_shape_change <- function(ord, ref_shape, PC,
horiz = TRUE,
gridPars = NULL, ...){
if(horiz){
op <- par(mfrow = c(1, 2), mar = c(0, 0 , 0, 0))
plotRefToTarget(M1 = ref_shape, M2 = ord$shapes[[PC]]$min,
gridPars = gridPars, ...)
plotRefToTarget(M1 = ref_shape, M2 = ord$shapes[[PC]]$max,
gridPars = gridPars, ...)
par(op)
} else {
op <- par(mfrow = c(2, 1), mar = c(0, 0 , 0, 0))
plotRefToTarget(M1 = ref_shape, M2 = ord$shapes[[PC]]$max,
gridPars = gridPars, ...)
plotRefToTarget(M1 = ref_shape, M2 = ord$shapes[[PC]]$min,
gridPars = gridPars, ...)
par(op)
}
}
plot_shape_change(ord, ref_shape = gpa$consensus, PC = 1, links = plethodon$links, method = "TPS")
plot_shape_change(ord, ref_shape = gpa$consensus, PC = 2, links = plethodon$links, method = "TPS", horiz = FALSE)
my_gridPar <- gridPar(tar.pt.size = 0.6, grid.lwd = 0.7)
library(cowplot)
gg_pca <- plot_grid(
~ plot_shape_change(ord, ref_shape = gpa$consensus, PC = 2,
horiz = FALSE, links = plethodon$links,
method = "TPS", gridPars = my_gridPar),
~ {plot(ord, bg = colvec, pch = 21, col = "grey20")
legend("topright", legend = levels(gp), bty = "n",
pch = 21, col = "grey20",
pt.bg = levels(as.factor(colvec)))},
NULL,
~ plot_shape_change(ord, ref_shape = gpa$consensus, PC = 1,
links = plethodon$links,
method = "TPS", gridPars = my_gridPar),
ncol = 2, rel_heights = c(5, 1), rel_widths = c(1, 4)
)
gg_pca
Если у вас есть данные о средних формах для каждого вида и данные о филогении (из любого источника), то можно изобразить эволюционные изменения формы
Этапы:
P. serratus, P. cinereus, P. shenandoah, P. hoffmani, P. virginia, P. nettingi, P. hubrichti, P. electromorphus, P. richmondi
data(plethspecies) str(plethspecies, vec.len = 2, give.attr = F)
## List of 2 ## $ land: num [1:11, 1:2, 1:9] 0.217 0.259 ... ## $ phy :List of 4 ## ..$ edge : int [1:16, 1:2] 10 10 11 12 12 ... ## ..$ Nnode : int 8 ## ..$ tip.label : chr [1:9] "P_serratus" "P_cinereus" ... ## ..$ edge.length: num [1:16] 15.17 3.84 ...
species_gpa <- gpagen(plethspecies$land) #GPA-alignment
## ## Performing GPA ## | | | 0% | |=============== | 25% | |============================== | 50% | |============================================================| 100% ## ## Making projections... Finished!
Филоморфопространство
pca_with_phylo <- gm.prcomp(species_gpa$coords, phy = plethspecies$phy) plot(pca_with_phylo, phylo = TRUE)
