Distance-based Redundancy Analysis, dbRDA

# Distance-based Redundancy Analysis, dbRDA
## Анализ и визуализация многомерных данных с использованием R
### Марина Варфоломеева
### Вадим Хайтов

---

## О чем эта лекция

- Обзор и взаимосвязи методов непрямой и прямой ординации
- Специфика данных сообществ в связи с ординацией, эффект подковы
- Экологически-осмысленные трансформации данных
- PCoA, отрицательные собственные числа и поправки для борьбы с ними
- tbRDA
- dbRDA

### Вы сможете

- Выбрать подходящий для данных метод прямой или непрямой ординации
- Идентифицировать эффект подковы и бороться с ним разными способами
- Проводить PCoA, tbRDA и dbRDA в R

---

# Подходы к анализу состава сообществ

Вспоминаем, что такое непрямая и прямая ординация

---

## Анализ данных о составе сообществ

**Классический подход**

**PCA**
- **Евклидово расстояние**
- Если есть нули в данных, то должны быть "осмысленными"
- Короткие градиенты. Эффект подковы на счетных данных для длинных градиентов
  
**CA**
- **Хи-квадрат расстояние**
- счетные данные, могут быть нули
- Короткие и длинные градиенты. Эффект дуги на длинных градиентах

]
.pull-right-66[
![1](images/dbRDA 2022-04-20 17.25.01_1.excalidraw.svg)
]

---

## Иногда можно преобразовать данные

**Подход, основанный на трансформации данных**

**tbPCA** --- transformation-based PCA

- Данные ---> Расстояние Хеллингера
- Матрица расстояний ---> Трансформация Хеллингера
]
.pull-right-66[
![1](images/dbRDA 2022-04-20 17.25.01_2.excalidraw.svg)
]

---

## Свобода выбора коэффициентов различия

**Многомерное шкалирование**

**nMDS** --- неметрическое многомерное шкалирование
- Не проекционный метод, используется информация всех изменений

]
.pull-right-66[
![1](images/dbRDA 2022-04-20 17.25.01_3.excalidraw.svg)
]

---

## Добавим внешние факторы --- прямая ординация

**Классический подход**

**RDA** 
- **Евклидово расстояние** между объектами
- только "короткие" градиенты; плохо работает на "длинных градиентах", где много нулей

**CCA**
- **Хи-квадрат расстояние** между объектами
- и "короткие", и "длинные" градиенты (с разным таксономическим составом на разных концах)
]

.pull-right-66[
![modified after Fig. 11.4a, p.648 in Legendre, Legendre, 2012](images/dbRDA 2022-04-20 18.00.29_1.excalidraw.svg)
.small[modified after Fig. 11.4, p.648 in Legendre, Legendre, 2012]
]

---

## А если хочется использовать другие коэффициенты?

**Подход, основанный на трансформации данных**

**tbRDA** --- transformation-based RDA (Legendre, Gallagher, 2001)

- Данные ---> Расстояние Хеллингера
- Матрица расстояний ---> Трансформация Хеллингера
]

.pull-right-66[
![modified after Fig. 11.4ab, p.648 in Legendre, Legendre, 2012](images/dbRDA 2022-04-20 18.00.29_2.excalidraw.svg)
.small[modified after Fig. 11.4, p.648 in Legendre, Legendre, 2012]
]

---

## Но ещё лучше перевести всё в Евклидово пространство

**Подход, основанный на расстояниях**

**dbRDA** --- distance-based RDA (Legendre, Anderson, 1999)

Можно использовать RDA для неевклидовых коэффициентов, если  при помощи PCoA (Principal coordinate analysis) перевести их в Евклидово пространство.

- Данные ---> Матрица расстояний ---> PCoA ---> RDA
]

.pull-right-66[
![modified after Fig. 11.4ab, p.648 in Legendre, Legendre, 2012](images/dbRDA 2022-04-20 18.00.29_3.excalidraw.svg)
.small[modified after Fig. 11.4, p.648 in Legendre, Legendre, 2012]
]

---

## Все эти методы --- это тот же RDA

**...но есть новые для нас элементы**

- tb-RDA
  - трансформация хорды
  - трансформация Хеллингера
- db-RDA
  - PCoA
  - проблемы с отрицательными собственными числами

]

.pull-right-66[
![modified after Fig. 11.4abс, p.648 in Legendre, Legendre, 2012 с изменениями](images/dbRDA 2022-04-20 18.00.29_4focus.excalidraw.svg)
.small[modified after Fig. 11.4, p.648 in Legendre, Legendre, 2012]
]

---

# Длинные градиенты

Что же это значит? В чем проблема с их анализом?

---

# PCA

https://youtu.be/ZDh97N6L3bU

---

# PCA с трансформацией Хелингера

https://youtu.be/DpZpldfnqpo

---

# CA

https://youtu.be/FrfyRhxG4Ug

---

# nMDS

https://youtu.be/rCDj5IAzYiM

---

background-image: url("images/Finnish_Reindeer_178137137.jpeg")
background-position: center
background-size: cover

# Пример: Растительность в сосновых лесах,<br/> где пасутся олени

---

## Растительность в сосновых лесах, где пасутся олени

Фрагмент из датасета (Henry et al. 1995).

- `varespec` --- покрытие 44 видов на 24 участках в северной Финляндии и на Кольском полуострове.
- `varechem` --- 14 переменных, описывающих условия среды.

(В исходном исследовании была еще информация о выпасе оленей)

Какие факторы среды определяют облик растительного сообщества?

]

.small[[Mathew Schwartz](https://upload.wikimedia.org/wikipedia/commons/f/fb/Finnish_Reindeer_%28178137137%29.jpeg), [CC BY 3.0](https://creativecommons.org/licenses/by/3.0), via&nbsp;Wikimedia&nbsp;Commons]
]
.pull-down[

]

???

Богатые лишайниками сосновые леса на песчаных почвах. Там пасутся полудомашние олени. Выпас скота влияет на растительность много где, здесь тоже.

nMDS: мхи и лишайники на противоположных концах ординации. Высокая пастбищная нагрузка - в середине.

---

## Знакомство с данными

```r
library("ggplot2")
theme_set(theme_minimal(base_size = 18))
library("cowplot")
library("vegan")
```

```
## Loading required package: permute
```

```
## Loading required package: lattice
```

```
## This is vegan 2.6-2
```

```r
data("varespec")
data("varechem")
head(varespec, 2)
```

```
##    Callvulg Empenigr Rhodtome Vaccmyrt Vaccviti Pinusylv Descflex
## 18     0.55    11.13        0     0.00    17.80     0.07        0
## 15     0.67     0.17        0     0.35    12.13     0.12        0
##    Betupube Vacculig Diphcomp Dicrsp Dicrfusc Dicrpoly Hylosple
## 18        0      1.6     2.07   0.00     1.62     0.00        0
## 15        0      0.0     0.00   0.33    10.92     0.02        0
##    Pleuschr Polypili Polyjuni Polycomm Pohlnuta Ptilcili Barbhatc
## 18     4.67     0.02     0.13        0     0.13     0.12        0
## 15    37.75     0.02     0.23        0     0.03     0.02        0
##    Cladarbu Cladrang Cladstel Cladunci Cladcocc Cladcorn Cladgrac
## 18    21.73    21.47     3.50     0.30     0.18     0.23     0.25
## 15    12.05     8.13     0.18     2.65     0.13     0.18     0.23
##    Cladfimb Cladcris Cladchlo Cladbotr Cladamau Cladsp Cetreric
## 18     0.25     0.23        0        0     0.08   0.02     0.02
## 15     0.25     1.23        0        0     0.00   0.00     0.15
##    Cetrisla Flavniva Nepharct Stersp Peltapht Icmaeric Cladcerv
## 18     0.00     0.12     0.02   0.62     0.02        0        0
## 15     0.03     0.00     0.00   0.85     0.00        0        0
##    Claddefo Cladphyl
## 18     0.25        0
## 15     1.00        0
```

```r
sum(is.na(varespec))
```

```
## [1] 0
```
]

---

## Задание 1

Сделайте PCA данных о составе сообщества

Сколько изменчивости объясняют первые две главные компоненты?

Нарисуйте график ординации

---

## Решение: PCA данных о составе сообщества

```r
mod_pca <- rda(varespec)
eigenvals(mod_pca)/sum(eigenvals(mod_pca))*100
```

```
##   PC1   PC2   PC3   PC4   PC5   PC6   PC7   PC8   PC9  PC10  PC11 
## 53.84 25.43  7.24  4.05  2.65  2.03  1.41  1.08  0.67  0.57  0.51 
##  PC12  PC13  PC14  PC15  PC16  PC17  PC18  PC19  PC20  PC21  PC22 
##  0.15  0.13  0.08  0.07  0.04  0.02  0.01  0.01  0.00  0.00  0.00 
##  PC23 
##  0.00
```

```r
biplot(mod_pca, scaling = 2)
```

Хорошо заметен "эффект подковы"

---

## Как исправить эффект подковы?

Все варианты основаны на выборе иного коэффициента различия вместо Евклидова расстояния:

- Корреспондентный анализ, CA (хи-квадрат)
- Трансформация данных
  - Расстояние Хеллингера
  - Хордальное расстояние
- Использование другого коэффициента различия
  - Коэффициент Брея-Куртиса

---

# Экологически-осмысленные трансформации

---

## Распределения обилия видов асимметричны

???

Широко известный факт, используется в моделях обилия видов (species-abundance models) (обзор моделей см. в работах He, Legendre, 1996, 2002).

---

## Степенные трансформации

`$y' = y^{0.5}$`; `$y' = y^{0.25}$`; `$y' = log(y + c),\ \text{обычно }c = 1$`

---

## После этих трансформаций эффект подковы "смазан"

**Но он не исчез**, т.к. не решена проблема двойных нулей.

```r
op <- par(mfrow = c(1, 3), mar = c(4, 4, 1.5, 0.5), cex = 1)
mod_pca <- rda(varespec)
biplot(mod_pca, scaling = 2, main = "сырые данные")
mod_pca <- rda(sqrt(varespec))
biplot(mod_pca, scaling = 2, main = "квадратный корень")
mod_pca <- rda(log(varespec + 1))
biplot(mod_pca, scaling = 2, main = "логарифм")
par(op)
```

---

## Хордальное расстояние

Orlóci, 1967 предложил использовать для анализа состава сообществ. Часто использовали в генетике (Cavalli-Sforza, Edwards, 1967).

`$D_{3}(\mathbf{x}_1, \mathbf{x}_2) = \sqrt{2\left( 1 - { \sum_{j=1}^p y_{1j}y_{2j} }\over{ \sqrt{\sum_{j = 1}^p y^2_{1j} \sum_{j = 1}^p y^2_{2j}} }\right)} = \sqrt{\sum_{j = 1}^p \left( {{y_{1j}} \over {\sqrt{\sum_{j = 1}^p y^2_{1j}}}} - {{y_{2j}}\over{\sqrt{\sum_{j = 1}^p y^2_{2j}}}} \right)^2}$` .fn[[*]]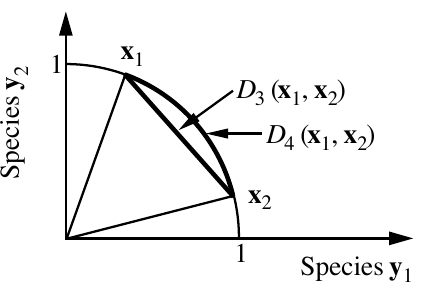

`$$0 \le D_{3} \le \sqrt{2}$$` 
- `$\sqrt{2}$` --- нет общих видов
- `$0$` --- одинаковая доля видов (но не обязательно численность)

= Евклидово расстояние после нормализации по строкам (вектор, деленный на длину вектора)
]

.footnote[
---------- 
[*] --- Legendre, Legendre, 2012 (коэффициент `$D_{3}$`, формула&nbsp;7.35,&nbsp;стр.&nbsp;301).
]

???

Legendre, Gallagher, 2001 говорят, что лучше расстояние Хеллингера.

---

## Расстояние Хеллингера

Описал Rao, 1995 (на основе интеграла Хеллингера, Hellinger, 1909)

`$\mathbf{D_{17}}(x_1, x_2) = \sqrt{\sum^p_{j = 1}\left[\sqrt{\frac{y_{1j}}{y_{1+}}}\sqrt{\frac{y_{2j}}{y_{2+}}}\right]}$` .fn[[*]]

`$$0 \le D_{3} \le \sqrt{2}$$`

Асимметричный коэффициент (нечувствителен к двойным нулям)

= хордальное расстояние, рассчитанное по корням из обилий видов

.footnote[
---------- 
[*] --- Legendre, Legendre, 2012 (коэффициент `$D_{17}$`, формула&nbsp;7.56,&nbsp;стр.&nbsp;310)
]

---

### Трансформация хорды

![Fig. 2 in Legendre, Gallagher, 2001](images/chord-trans_LegendreGallagher2001_Fig2.png)

`$y'_{ij} = \frac {y_{ij}} {\sqrt{\sum_{j = 1}^p y^2_{ij}}}$`

Тр. хорды + Евклидово расстояние = хордальное расстояние

]

### Трансформация Хеллингера

![Fig.7.7 in Legendre, Legendre, 2012](images/hellinger-trans_LegendreLegendre2012_Fig7.7.png)
.small[Fig.7.7 in Legendre, Legendre, 2012]

`$y'_{ij} = \sqrt{\frac{y_{ij}}{y_{i+}}}$`

Тр. Хеллингера + Евклидово расстояние = расстояние Хеллингера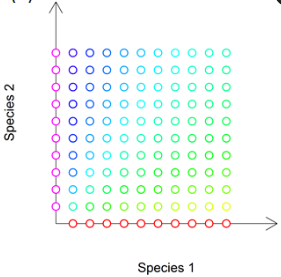

]

???

![120 сообществ](images/hellinger-trans_david-zeleny-b.png)
![трансформация Хеллингера](images/hellinger-trans_david-zeleny-d.png)
.small[
by [David Zelený](https://davidzeleny.net/blog/2022/03/17/)
]

---

## После трансформаций эффект подковы может исчезнуть

**Но не обязательно**, он останется, если "длинный градиент"

```r
op <- par(mfrow = c(1, 3), mar = c(4, 4, 1.5, 0.5), cex = 1)
mod_pca <- rda(varespec)
biplot(mod_pca, scaling = 2, main = "сырые данные")
mod_pca <- rda(decostand(varespec, method = "normalize"))
biplot(mod_pca, scaling = 2, main = "хордальное расст.")
mod_pca <- rda(decostand(varespec, method = "hellinger"))
biplot(mod_pca, scaling = 2, main = "расст. Хеллингера")
par(op)
```

---

# PCoA

Учимся использовать неевклидовы меры различий в ординации

---

## Principal Coordinate Analysis, PCoA

Gower, 1966

= метрическое многомерное шкалирование, классическое шкалирование

**Цель: создать Евклидово изображение неевклидова пространства, сохраняя отношения между объектами**.

Потенциально можно использовать любую меру различий, даже неевклидову.

Хорошо работает, если исходный коэффициент .red[метрический] (выполняется неравенство треугольника). Если .red[неметрический] --- могут быть проблемы.

---

## PCoA, часть 1

![PCoA](images/dbRDA 2022-04-22 14.47.44_1.excalidraw.svg)

Матрицу коэффициентов различия `$D = [D_{hi}]$` преобразуем в матрицу `$A = [a_{hi}]$`:
`$$a_{hi} = - \frac{1}{2} D^2_{hi}$$`
???

---

## PCoA, часть 2

![PCoA](images/dbRDA 2022-04-22 14.47.44_2.excalidraw.svg)

Центрируем матрицу `$A$` методом Говера, чтобы получить матрицу `$\Delta_{1} = [\delta_{hi}]$`:
`$$\delta_{hi} = a_{hi} - \bar a_{h} - \bar a_{i} + \bar a$$`
- `$\bar a_h$`  и `$\bar a_i$` --- среднее по строке и по столбцу `$A$`, 
- `$\bar a$` --- общее среднее матрицы `$A$`

???

В виде матриц это можно записать так:
`$\Delta _1 = \left( I - \frac{\mathbf{11'}}{n} \right) A \left( I - \frac{\mathbf{11'}}{n} \right)$`, 
- `$I$` --- единичная матрица `$n \times n$`
- `$\mathbf{1}$` --- единичный вектор-столбец длиной `$n$`

---

## PCoA, часть 3

![PCoA](images/dbRDA 2022-04-22 14.47.44_3.excalidraw.svg)

Спектральное разложение Говеровски-центрированной матрицы `$\Delta_{1}$`:
- собственные числа `$\lambda_k$`
- нормализованные собственные векторы `$\mathbf u_k$` (матрица `$\mathbf U$`)

Собственные векторы умножаются на корень из их собственных чисел. Минимум одно собственное число равно нулю (т.к.  `$\Delta_{1}$` центрирована).

Исходные переменные можно проецировать в пространство ординации.

???

После масштабирования собственные векторы длиной квадратный корень из их собственных чисел `$\sqrt{\mathbf{u}'_k \mathbf{u}_k} = \sqrt{\lambda_k}$`.

Исходные переменные не используются в PCA, но их можно спроецировать в пространство ординации.
`$S_{pc} = \frac{1}{(n - 1)} Y_c'Y_{st}$`
`$U_{proj} = \sqrt{n - 1} S_{pc} \Lambda^{-0.5}$`
`$Y_c$` - центрированная матрица данных (или объясняющих переменных). ЕЕ нужно стандартизовать, если переменные в разных шкалах. Может содержать любой набор вспомогательных количественных данных.
`$U_{st}$` - Матрица собственных векторов PCoA или ее кусочек (стандартизована по столбцам).
`$S_{pc}$` - матрица ковариаций `$Y$` и `$U_{st}$`
`$U_{proj}$` - строки матрицы - это p переменных, которые нужно добавить на биплот, столбцы - это координаты.

---

## PCoA в R

```r
#
#
d_eucl <- vegdist(varespec, method = "euclidean")
mod_pcoa_eucl <- cmdscale(d_eucl, k = nrow(varespec) - 1, eig = TRUE)
ordiplot(mod_pcoa_eucl, type = "t")
```

```
## species scores not available
```

]
.panel[.panel-name[Хордальное р.]

```r
#
varespec_norm <- decostand(varespec, "normalize")
d_chord <- vegdist(varespec_norm, method = "euclidean")
mod_pcoa_chord <- cmdscale(d_chord, k = nrow(varespec) - 1, eig = TRUE)
ordiplot(mod_pcoa_chord, type = "t")
```

```
## species scores not available
```

]
.panel[.panel-name[Р. Хеллингера]

```r
#
varespec_hel <- decostand(varespec, "hellinger")
d_hel <- vegdist(varespec_hel, method = "euclidean")
mod_pcoa_hel <- cmdscale(d_hel, k = nrow(varespec) - 1, eig = TRUE)
ordiplot(mod_pcoa_hel, type = "t")
```

```
## species scores not available
```

]
.panel[.panel-name[Коэф. Брея-Куртиса]

```r
d_bray <- vegdist(varespec,  method = "bray")
mod_pcoa_bray <- cmdscale(d_bray,  k = nrow(varespec) - 1, eig = TRUE)
```

```
## Warning in cmdscale(d_bray, k = nrow(varespec) - 1, eig = TRUE): only
## 15 of the first 23 eigenvalues are > 0
```

```r
ordiplot(mod_pcoa_bray, type = "t")
```

```
## species scores not available
```

<img src="12_dbRDA_files/figure-html/pcoa-bray-1.png" style="display: block; margin: auto;" />
]
]

---

## Задание 2

Получите собственные числа из анализа PCoA по матрице коэффициентов Брея-Куртиса.

---

## Решение: Собственные числа

Посмотрите на них внимательно. Что в них странного?

```r
eigenvals(mod_pcoa_bray)
```

```
##  [1]  1.7552  1.1334  0.4429
##  [4]  0.3698  0.2454  0.1961
##  [7]  0.1751  0.1284  0.0972
## [10]  0.0760  0.0637  0.0583
## [13]  0.0395  0.0173  0.0051
## [16]  0.0000 -0.0004 -0.0065
## [19] -0.0133 -0.0254 -0.0375
## [22] -0.0480 -0.0537 -0.0741
```

---

# Отрицательные собственные числа

Что в них плохого и как с ними бороться

---

## Причины появления отрицательных собственых чисел

- Использование полуметрических или неметрических мер различия.
- Пропущенные значения (вернее, их обработка некоторыми коэффициентами: Gower, Estabrook & Rogers, Legendre & Chodorowski) 
- Неевклидовость (non-Euclideanarity, Gower, 1982, 1985)

Отрицательные собственные числа для более высоких измерений, но хорошее отображение в первых нескольких измерениях.

---

## Вспомним определения

.content-box-green[
.green[**Метрики**] --- коэффициенты, у которых есть свойства адекватность, позитивность и симметричность, а так же выполняется неравенство треугольника.
]

.content-box-purple[
.purple[**Неметрики**] --- могут принимать отрицательные значения (не обладают свойством позитивности)
]

Если у коэффициента отсутствуют какие-либо из свойств метрик, то такое пространство не получится изобразить в Евклидовом пространстве. Признаком этого являются .red[**отрицательные собственные числа**].

.content-box-red[
.red[**Неевклидовы коэффициенты**] --- пространство, описываемое неевклидовым коэффициентом, невозможно описать в Евклидовом пространстве.
]

---

## Последствия:

Биплоты с разными поправками будут в общих чертах похожи.

Отрицательные собственные числа влияют на вероятность возникновения ошибок I рода в тестах значимости.

???

Методы коррекции pp. 502-504 in Legendre, Legendre, 2012

---

## Боремся с отрицательными собственными числами

- Трансформация матрицы различий.

- Поправка к матрице различий.

---

## Первый вариант --- трансформировать матрицу различий

Для некоторых (даже неевклидовых) коэф. различия есть трансформации, которые переводят их в Евклидовы.

Пример для свойств коэффициентов сходства.

| Коэф. сходства | `$D = 1-S$` | `$D = 1 - S$` <br/> Евклид. | `$D = \sqrt{1 - S}$` <br/> метрика | `$D = \sqrt{1 - S}$` <br/> Евклид. |
| ---- | ---- | ---- | ---- | ---- |
| Simple matching | метрика | **нет** | да | да |
| Жаккард | метрика | **нет** | да | да |
| Соренсен | полуметрика | **нет** | да | да |
| Кульчинский | неметрика | **нет** | **нет** | **нет** |

---

## Первый вариант --- трансформировать матрицу различий

Для некоторых (даже неевклидовых) коэф. различия есть трансформации, которые переводят их в Евклидовы.

А этот пример --- для коэффициентов различия.

| Коэф. различия | `$D$` | `$D$` <br/> Евклид. | `$\sqrt{D}$` <br/> метрика | `$\sqrt{D}$` <br/> Евклид. |
| ---- | ---- | ---- | ---- | ---- |
| Евклидово расст. | метрика | да | да | да |
| Расст. по Манхеттену | метрика | **нет** | да | да |
| Расст. хорды | метрика | да | да | да |
| Хи-квадрат | метрика | да | да | да |
| Расст. Хеллингера | метрика | да | да | да |
| Коэф Брея-Куртиса | полуметрика | **нет** | да | да |

???

Table 7.2 in Legendre, Legendre, 2012

---

## Второй вариант --- внести поправку

При неевклидовости можно сделать поправку к матрице различий (но не слишком большую):

.content-box-purple[
.purple[**Caillez correction**] --- добавить константу к суб- и супрадиагональным элементам матрицы различий `$\mathbf{D}$`.

Завышена вероятность ошибки I рода в ANOVA (Legendre, Anderson, 1999).
]
.content-box-green[
.green[**Lingoes correction**] --- добавить константу к квадратам суб- и супрадиагональных элементов матрицы различий `$\mathbf{D}$`.

Несмещенная вероятность ошибки I рода в ANOVA.
]

???

see 5.5.1 in Borcard, Legendre, 2018

---

## Поправка Сailliez есть в `vegan::cmdscale()`

И эта поправка --- единственная в `cmdscale()`

```r
d_bray <- vegdist(varespec,  method = "bray")
mod_pcoa_bray <- cmdscale(d_bray,  k = nrow(varespec) - 1, eig = TRUE)

eigenvals(mod_pcoa_bray)
```

```
##  [1]  1.7552  1.1334  0.4429  0.3698  0.2454  0.1961  0.1751  0.1284
##  [9]  0.0972  0.0760  0.0637  0.0583  0.0395  0.0173  0.0051  0.0000
*## [17] -0.0004 -0.0065 -0.0133 -0.0254 -0.0375 -0.0480 -0.0537 -0.0741
```

]
.panel[.panel-name[Сailliez]

```r
d_bray <- vegdist(varespec,  method = "bray")
mod_pcoa_bray_cai <- cmdscale(d_bray,  k = nrow(varespec) - 1, eig = TRUE, 
                              add = TRUE) # <<-

eigenvals(mod_pcoa_bray_cai)
```

```
##  [1] 2.6382 1.7634 0.7727 0.6529 0.4733 0.4214 0.3712 0.2990
##  [9] 0.2532 0.2076 0.1932 0.1876 0.1498 0.1112 0.0981 0.0924
*## [17] 0.0806 0.0684 0.0434 0.0352 0.0306 0.0209 0.0000 0.0000
```

]
]

---

## Строим график по данным с поправкой Сailliez

Нанесем на график .red[взвешенные средние видов].

<img src="12_dbRDA_files/figure-html/pcoa-bray-cai-plot-1.png" style="display: block; margin: auto;" />
]
.panel[.panel-name[Код]

```r
ordiplot(scores(mod_pcoa_bray_cai, choices = c(1, 2)), type = "t")
abline(h = 0, lty = 1, lwd = 0.5)
abline(v = 0, lty = 1, lwd = 0.5)

# Взвешенные средние видов
varespec_wa <- wascores(mod_pcoa_bray_cai$points[, 1:2], varespec)
text(varespec_wa, rownames(varespec_wa), cex = 0.7, col = "red")
```
]
]

---

## Задание 3

Нанесите на график ординации .purple[проекции переменных среды] при помощи `envfit()`.

Используйте только переменные, значимо связанные со структурой сообществ.

---

## Решение: График по данным с поправкой Сailliez

На график нанесены .red[взвешенные средние видов] и .purple[проекции переменных среды].

<img src="12_dbRDA_files/figure-html/pcoa-bray-cai-plot-2-1.png" style="display: block; margin: auto;" />
]
.panel[.panel-name[Код]

```r
ordiplot(scores(mod_pcoa_bray_cai, choices = c(1, 2)), type = "t")
abline(h = 0, lty = 1, lwd = 0.5)
abline(v = 0, lty = 1, lwd = 0.5)

# Взвешенные средние видов
varespec_wa <- wascores(mod_pcoa_bray_cai$points[, 1:2], varespec)
text(varespec_wa, rownames(varespec_wa), cex = 0.7, col = "red")

# Решение 3 -----------------------------------------------------
# Проекции переменных среды ->> таблица
mod_pcoa_bray_cai_env <- envfit(mod_pcoa_bray_cai, varechem)

# Значимые наносим на график
plot(mod_pcoa_bray_cai_env, p.max = 0.05, col = "darkviolet")
# --------------------------------------------------------------
```
]
.panel[.panel-name[Таблица результатов envfit]

```r
mod_pcoa_bray_cai_env
```

```
## 
## ***VECTORS
## 
##            Dim1   Dim2   r2 Pr(>r)    
## N         0.135  0.991 0.23  0.059 .  
## P         0.487 -0.873 0.27  0.032 *  
## K         0.726 -0.687 0.16  0.158    
## Ca        0.685 -0.729 0.35  0.008 ** 
## Mg        0.726 -0.687 0.28  0.027 *  
## S         0.211 -0.977 0.11  0.292    
## Al       -0.987  0.159 0.52  0.002 ** 
## Fe       -0.974  0.225 0.46  0.001 ***
## Mn        0.933 -0.360 0.44  0.004 ** 
## Zn        0.761 -0.649 0.19  0.114    
## Mo       -0.706  0.708 0.05  0.590    
## Baresoil  0.950  0.312 0.25  0.046 *  
## Humdepth  0.914 -0.405 0.45  0.003 ** 
## pH       -0.992 -0.129 0.24  0.057 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Permutation: free
## Number of permutations: 999
```

]
]

---

## Если нужна поправка Lingoes --- `ape::pcoa()`

```r
library(ape) # здесь есть обе поправки к PCoA
d_bray <- vegdist(varespec,  method = "bray")
```

```r
mod_pcoa_raw <- pcoa(d_bray)
mod_pcoa_raw$values$Eigenvalues
```

```
##  [1]  1.7552165  1.1334455  0.4429018
##  [4]  0.3698054  0.2453532  0.1960921
##  [7]  0.1751131  0.1284467  0.0971594
## [10]  0.0759601  0.0637178  0.0583225
## [13]  0.0394934  0.0172699  0.0051011
## [16]  0.0000000 -0.0004131 -0.0064654
## [19] -0.0133147 -0.0253944 -0.0375105
## [22] -0.0480069 -0.0537146 -0.0741390
```
]
.pull-right[

```r
biplot.pcoa(mod_pcoa_raw, varespec)
```

<img src="12_dbRDA_files/figure-html/neg-eig-nocor-1.png" style="display: block; margin: auto;" />
]
]
.panel[.panel-name[Сailliez]
.pull-left[

```r
mod_pcoa_cai <- pcoa(d_bray, 
              correction = "cailliez")
mod_pcoa_cai$values$Corr_eig
```

```
##  [1] 2.63820 1.76344 0.77272
##  [4] 0.65286 0.47325 0.42136
##  [7] 0.37118 0.29904 0.25324
## [10] 0.20761 0.19322 0.18756
## [13] 0.14980 0.11123 0.09814
## [16] 0.09244 0.08057 0.06839
## [19] 0.04338 0.03522 0.03057
## [22] 0.02086 0.00000 0.00000
```
]
.pull-right[

```r
biplot.pcoa(mod_pcoa_cai, varespec)
```

<img src="12_dbRDA_files/figure-html/neg-eig-cailliez-1.png" style="display: block; margin: auto;" />
]
]
.panel[.panel-name[Lingoes]
.pull-left[

```r
mod_pcoa_lin <- pcoa(d_bray, 
                correction = "lingoes")
mod_pcoa_lin$values$Corr_eig
```

```
##  [1] 1.82936 1.20758 0.51704
##  [4] 0.44394 0.31949 0.27023
##  [7] 0.24925 0.20259 0.17130
## [10] 0.15010 0.13786 0.13246
## [13] 0.11363 0.09141 0.07924
## [16] 0.07373 0.06767 0.06082
## [19] 0.04874 0.03663 0.02613
## [22] 0.02042 0.00000 0.00000
```
]
.pull-right[

```r
biplot.pcoa(mod_pcoa_lin, varespec)
```

<img src="12_dbRDA_files/figure-html/neg-eig-lingoes-1.png" style="display: block; margin: auto;" />
]]
]

---

## Сравнение методов непрямой ординации

PCA
- Короткие градиенты
- Евклидово расстояние. Нужны "осмысленные" нули (double-zero problem).
- Представляет отношения между объектами в Евклидовом пространстве
- Главные компоненты --- функции исходных признаков

PCoA
- "Теряет" информацию о неевклидовой части матрицы D (Legendre, Legendre, 2012)
- Линейная трансформация расстояний между объектами: главные координаты --- функции исходных признаков, выраженных посредством расстояний

CA
- Короткие и длинные градиенты
- Хи-квадрат

nMDS
- Лучше отображает многомерное пространство, чем PCoA.
- Сохраняются ранги расстояний между объектами.
- Нелинейная трансформация между объектами.

---

# Это всё была непрямая ординация

## А дальше --- прямая ординация

---

# tbRDA

RDA по трансформированным данным

---

## Transformation-based RDA, tbRDA

![tbRDA](images/dbRDA 2022-04-23 09.29.03.excalidraw.svg)

---

### Функция для рисования графиков ординации в ggplot

```r
# ordiggplot Рисует график ординации из vegan в ggplot
ordiggplot <- function(mod, lab_size = 5, lab_var_size = 6,
                       line_size = 0.5, point_size = 2,
                      plot_sites = TRUE, plot_species = TRUE,
                      plot_centroids = TRUE, plot_biplot = TRUE,
                      plot_factorbiplot = TRUE, ...){
  mod_dat <- scores(mod, tidy = TRUE, ...)
  ax_names <- colnames(mod_dat)[1:2]
  names(mod_dat)[1:2] <- c("X", "Y")
  mod_eig <- round(eigenvals(mod) / mod$tot.chi * 100, 2)
  ar <- arrow(angle = 10, length = unit(2, "mm"), type = "closed")
  gg <- ggplot() +
    geom_hline(yintercept = 0, colour = "grey70", size = 0.25) +
    geom_vline(xintercept = 0, colour = "grey70", size = 0.25)
  if(any(mod_dat$score == "sites" & plot_sites)) {
      gg <- gg +
      geom_point(data = filter(mod_dat, score == "sites"),
                 aes(x = X, y = Y), size = point_size) +
      geom_text(data = filter(mod_dat, score == "sites"),
                aes(x = X, y = Y, label = label),
                size = lab_size, hjust = -0.7,
                colour = "grey40")
  }
  if(any(mod_dat$score == "species" & plot_species)) {
      gg <- gg +
        geom_segment(data = filter(mod_dat, score == "species"),
                   aes(x = 0, y = 0, xend = X, yend = Y),
                   size = line_size, colour = "orangered", arrow = ar) +
        geom_text(data = filter(mod_dat, score == "species"),
                  aes(x = X, y = Y, label = label),
                  size = lab_size, hjust = 1.3, vjust = 0.4,
                  colour = "orangered")
  }
  if(any(mod_dat$score == "centroids" & plot_centroids)) {
    gg <- gg + geom_point(data = filter(mod_dat, score == "centroids"),
               aes(x = X, y = Y),
               shape = 13, size = 3,
               colour = "grey20") +
      geom_text(data = filter(mod_dat, score == "centroids"),
                aes(x = X, y = Y, label = label),
                size = lab_var_size, hjust = -0.2,
                colour = "grey20")
  }
  if(any(mod_dat$score == "factorbiplot" & plot_factorbiplot)) {
    gg <- gg + geom_point(data = filter(mod_dat, score == "factorbiplot"),
                          aes(x = X, y = Y),
                          shape = 19, size = 0.5,
                          colour = "blue") +
      geom_text(data = filter(mod_dat, score == "factorbiplot"),
                aes(x = X, y = Y, label = label),
                size = lab_var_size, hjust = -0.2,
                colour = "blue")
  }
  if(any(mod_dat$score == "biplot" & plot_biplot)) {
    gg <- gg + geom_segment(data = filter(mod_dat, score == "biplot"),
                 aes(x = 0, y = 0, xend = X, yend = Y),
                 size = line_size, colour = "blue",  arrow = ar) +
      geom_text(data = filter(mod_dat, score == "biplot"),
                aes(x = X, y = Y, label = label),
                size = lab_var_size, hjust = -0.2,
                colour = "blue")
  }
  gg + coord_cartesian() +
      labs(x = paste0(ax_names[1], " (", mod_eig[1], "%)"),
           y = paste0(ax_names[2], " (", mod_eig[2], "%)"))
  }
```
]

---

## tbRDA с расстоянием Хеллингера

```r
mod_tbrda <- rda(decostand(varespec, method = 'hellinger') ~  
                   Mn + Baresoil + N, data = varechem)

eigenvals(mod_tbrda)/sum(eigenvals(mod_tbrda))
```

```
##    RDA1    RDA2    RDA3     PC1     PC2     PC3     PC4     PC5 
## 0.21529 0.07364 0.03424 0.22379 0.14284 0.07402 0.05034 0.04629 
##     PC6     PC7     PC8     PC9    PC10    PC11    PC12    PC13 
## 0.02925 0.02751 0.02027 0.01602 0.01328 0.00973 0.00641 0.00517 
##    PC14    PC15    PC16    PC17    PC18    PC19    PC20 
## 0.00351 0.00265 0.00166 0.00161 0.00120 0.00087 0.00039
```
]
.panel[.panel-name[График]

```r
# ordiggplot(mod_tbrda, scaling = 1)
ordiggplot(mod_tbrda, scaling = 2) + aes(colour = varechem$Mn)
```

<img src="12_dbRDA_files/figure-html/tbrda-scaling-2-1.png" style="display: block; margin: auto;" />
]
.panel[.panel-name[ANOVA]

```r
anova(mod_tbrda, by = "mar")
```

```
## Permutation test for rda under reduced model
## Marginal effects of terms
## Permutation: free
## Number of permutations: 999
## 
## Model: rda(formula = decostand(varespec, method = "hellinger") ~ Mn + Baresoil + N, data = varechem)
##          Df Variance    F Pr(>F)   
## Mn        1   0.0492 3.99  0.004 **
## Baresoil  1   0.0303 2.46  0.036 * 
## N         1   0.0225 1.83  0.112   
## Residual 20   0.2468               
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
]
]

---

# dbRDA

Карт-бланш (ну, почти) на коэффициенты различия

---

## Distance-based RDA, dbRDA

Используется для анализа "неевклидовых" матриц различия

.pull-left[
Для количественных признаков:
  - асимметричный коэф. Говера
  - коэф Уиттакера
  - расстояние Канберра 
  - коэф. Брея-Куртиса, и т.п.
  
Для бинарных признаков:
  - коэф. Соренсена
  - коэф. Жаккара, и т.д.
  ]
.pull-right[
Для других типов данных:
  - симметричный коэф. Говера
  - коэф. Эстабрука-Роджерса
  - обобщенное расстояние Махаланобиса для групп
]

![dbRDA](images/dbRDA 2022-04-23 09.41.54_1.excalidraw.svg)

???

Legendre, Legendre, 2012

---

## Два варианта расчетов dbRDA в `vegan`

`vegan::capscale()` --- смещенная вероятность ошибки I рода в многофакторных ANOVA.
.small[
- .purple[Caillez correction] --- `add = "cailliez"`
- .green[Lingoes correction] --- `add = "lingoes"`
  ]
]
.pull-right[
**Новый вариант**  
(McArdle, Anderson, 2001)

`vegan::dbRDA()` --- правильная вероятность ошибки I рода в многофакторных ANOVA.
  - Виды нельзя добавить непосредственно на график.
]

![dbRDA](images/dbRDA 2022-04-23 09.41.54_2.excalidraw.svg)

---

## dbRDA по матрице коэффициентов Брея-Куртиса

```r
mod_dbrda_lingoes <- capscale(varespec ~ Mn + Baresoil + N, 
                              distance = "bray", data = varechem, add = TRUE)

eigenvals(mod_dbrda_lingoes)/sum(eigenvals(mod_dbrda_lingoes))
```

```
##    CAP1    CAP2    CAP3    MDS1    MDS2    MDS3    MDS4    MDS5 
## 0.16464 0.07210 0.05017 0.16860 0.13427 0.07332 0.05147 0.04711 
##    MDS6    MDS7    MDS8    MDS9   MDS10   MDS11   MDS12   MDS13 
## 0.03875 0.03134 0.02587 0.02299 0.02057 0.01895 0.01589 0.01378 
##   MDS14   MDS15   MDS16   MDS17   MDS18   MDS19   MDS20 
## 0.01259 0.01080 0.00971 0.00668 0.00573 0.00339 0.00128
```
]

```r
# ordiggplot(mod_dbrda_lingoes, scaling = 1)
ordiggplot(mod_dbrda_lingoes, scaling = 2) + aes(colour = varechem$Mn)
```

<img src="12_dbRDA_files/figure-html/dbrda-scaling-2-1.png" style="display: block; margin: auto;" />
]

```r
anova(mod_dbrda_lingoes, by = "mar")
```

```
## Permutation test for capscale under reduced model
## Marginal effects of terms
## Permutation: free
## Number of permutations: 999
## 
## Model: capscale(formula = varespec ~ Mn + Baresoil + N, data = varechem, distance = "bray", add = TRUE)
##          Df SumOfSqs    F Pr(>F)   
## Mn        1     0.70 3.16  0.003 **
## Baresoil  1     0.51 2.29  0.026 * 
## N         1     0.42 1.91  0.050 * 
## Residual 20     4.46               
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
]
]

---

## Summary

- Данные, описывающие состав сообщества:
  - имеют асимметричное распределение,
  - содержат много нулей,
  - нули не имеют особого смысла (виды отсутствуют по разным причинам).

- В силу этих свойств:
  - для описания сообществ не подходит Евклидово расстояние,
  - для данных, собранных вдоль длинных экологических градиентов, на ординации может возникать эффект подковы.

- Экологические данные можно трансформировать:
  - степенные трансформации избавят от асимметрии
  - есть трансформации, позволяющие уйти от Евклидова расстояния
  - некоторые неевклидовы коэффициенты трансформируются в Евклидовы.

- PCoA позволяет изобразить пространство любого коэффициента в Евклидовом пространстве. Но, чтобы в ANOVA были правильные вероятности ошибок I рода, не должно быть отрицательных собственных чисел (есть поправки).
- Благодаря PCoA можно использовать в dbRDA любые коэффициенты различия.

---

background-image: url("images/Lac_des_Brenets_2008.jpg")
background-position: center
background-size: cover

# Задание: Рыбы в реке Ду, Франция

---

## Рыбы в реке Ду, Франция

Verneaux (1973) предложил использовать сообщества рыб в качестве индикаторов состояния рек и ручьев.

- `doubs$fish` --- Обилие 27 видов рыб в 30 точках на реке Ду
- `doubs$env` --- 11 характеристик условий среды
- `doubs$xy` --- Координаты точек

Проанализируйте, какие факторы среды определяют облик сообществ рыб в реке Ду, если удалить влияние географической близости точек сбора.

```r
data("doubs", package = "ade4")
help("doubs", package = "ade4")
```

]

.pull-right[
![Lac des Brenets, Canton of Neuchâtel](images/Lac_des_Brenets_2008.jpg)
.small[[Schaffhausen](https://commons.wikimedia.org/wiki/File:Lac_des_Brenets_2008.jpg), Public domain, via Wikimedia Commons]
]

???

Река Ду - приток Соны. Находится на юго-востоке Франции (Бургундия) и западе Швейцарии. Исток в горах Юра.

По итогам диссертации Верно предложил классифицировать на 4 зоны: 
- зона форели (trout zone) --- ненарушенные, хорошо оксигенированные и олиготрофные
- grayling zone, 
- barbel zone, 
- bream zone --- эвтрофные и бедные кислородом воды

Verneaux, J. (1973) Cours d'eau de Franche-Comté (Massif du Jura). Recherches écologiques sur le réseau hydrographique du Doubs. Essai de biotypologie. Thèse d'état, Besançon. 1–257.

Borcard, D., Gillet, F. & Legendre, P. (2011) Numerical Ecology with R. Springer, UseR! Edition.

---

## Что почитать

* Legendre P., Legendre L. (2012) Numerical ecology. Second english edition. Elsevier, Amsterdam.
- Oksanen, J. (2022). Design decisions and implementation details in vegan. Vignette of the package vegan. R package version 2.6-2.